题目内容
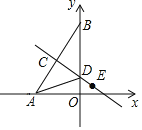
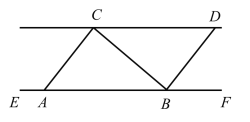
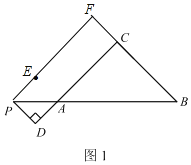
【题目】在△ABC中,∠C=90°,AC=BC,点P在线段BA的延长线上,作PD⊥AC,交AC的延长线于点D,点D关于直线AB的对称点为E,连接PE并延长PE到点F,使EF=AC,连接CF.
(1)依题意补全图1;
(2)求证:AD=CF;
(3)若AC=2,点Q在直线AB上,写出一个AQ的值,使得对于任意的点P总有QD=QF,并证明.
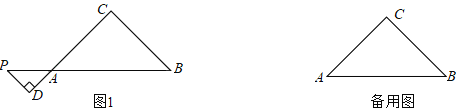
【答案】(1)见解析;(2)见解析;(3)AQ=![]() ,证明见解析.
,证明见解析.
【解析】
(1)依照题意,补全图形即可;
(2)通过证明四边形DCFP是矩形,可得PD=CF,由等腰直角三角形的性质可得AD=PD=CF;
(3)通过证明△DAQ≌△FCQ,可得QD=QF.
(1)补全图形,如图1所示:
(2)∵∠C=90°,AC=BC,
∴∠B=∠CAB=45°,
∵PD⊥AC,
∴∠PDA=90°,
∴∠DPA=90°﹣∠PAD=45°=∠DAP,
∴AD=DP,
∵点D关于直线AB的对称点为E,
∴∠FPA=∠DPA=45°,PE=PD,
∴∠DPF=90°,
∴∠DPF+∠D=180°,
∴PF//CD,
又∵EF=AC,
∴EF+PE=AC+AD,
即PF=CD,
∴PF![]() CD,
CD,
∴四边形PDCF是平行四边形,
又∵∠PDA=90°,
∴四边形DCFP是矩形,
∴PD=CF,
∴AD=CF;
(3)AQ=![]() ,
,
理由如下:如图2,连接CQ,
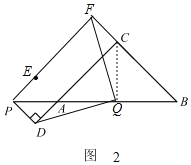
∵∠C=90°,AC=BC=2,
∴AB=2![]() ,∠B=∠CAB=45°,
,∠B=∠CAB=45°,
∵AQ=![]() ,
,
∴AQ=BQ,
又∵∠C=90°,AC=BC=2,
∴CQ=AQ=BQ,∠QCA=∠CAQ=45°,
∴∠DAQ=∠QCF=135°,
又∵AD=CF,
∴△DAQ≌△FCQ(SAS),
∴FQ=DQ.

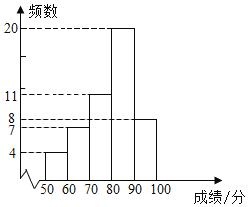
【题目】为了解某社区居民掌握民法知识的情况,对社区内的甲、乙两个小区各500名居民进行了测试,从中各随机抽取50名居民的成绩(百分制)进行整理、描述、分析,得到部分信息:
a.甲小区50名居民成绩的频数直方图如下(数据分成5组:50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100);
b.图中,70≤x<80组的前5名的成绩是:79 79 79 78 77
c.图中,80≤x<90组的成绩如下:
82 | 83 | 84 | 85 | 85 | 86 | 86 | 86 | 86 | 86 |
86 | 86 | 86 | 87 | 87 | 87 | 88 | 88 | 89 | 89 |
d.两组样本数据的平均数、中位数、众数、优秀率(85分及以上)、满分人数如下表所示:
小区 | 平均数 | 中位数 | 众数 | 优秀率 | 满分人数 |
甲 | 78.58 | 84.5 | a | b | 1 |
乙 | 76.92 | 79.5 | 90 | 40% | 4 |
根据以上信息,回答下列问题:
(1)求表中a,b的值;
(2)请估计甲小区500名居民成绩能超过平均数的人数;
(3)请尽量从多个角度,分析甲、乙两个小区参加测试的居民掌握民法知识的情况.