题目内容
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E、B.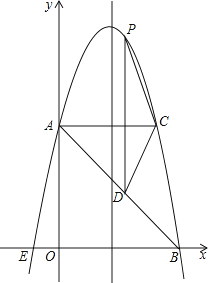
(1)求二次函数y=ax2+bx+c的表达式;
(2)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行与y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积;
(3)若点M在抛物线上,点N在其对称轴上,使得以A、E、N、M为顶点的四边形是平行四边形,且AE为其一边,求点M、N的坐标.
【答案】
(1)
解:设抛物线解析式为y=a(x﹣2)2+9,
∵抛物线与y轴交于点A(0,5),
∴4a+9=5,
∴a=﹣1,
y=﹣(x﹣2)2+9=﹣x2+4x+5
(2)
解:当y=0时,﹣x2+4x+5=0,
∴x1=﹣1,x2=5,
∴E(﹣1,0),B(5,0),
设直线AB的解析式为y=mx+n,
∵A(0,5),B(5,0),
∴m=﹣1,n=5,
∴直线AB的解析式为y=﹣x+5;
设P(x,﹣x2+4x+5),
∴D(x,﹣x+5),
∴PD=﹣x2+4x+5+x﹣5=﹣x2+5x,
∵AC=4,
∴S四边形APCD= ![]() ×AC×PD=2(﹣x2+5x)=﹣2x2+10x,
×AC×PD=2(﹣x2+5x)=﹣2x2+10x,
∴当x=﹣ ![]() =
= ![]() 时,
时,
∴S四边形APCD最大= ![]()
(3)
解:如图,
过M作MH垂直于对称轴,垂足为H,
∵MN∥AE,MN=AE,
∴△HMN≌△AOE,
∴HM=OE=1,
∴M点的横坐标为x=3或x=1,
当x=1时,M点纵坐标为8,
当x=3时,M点纵坐标为8,
∴M点的坐标为M1(1,8)或M2(3,8),
∵A(0,5),E(﹣1,0),
∴直线AE解析式为y=5x+5,
∵MN∥AE,
∴MN的解析式为y=5x+b,
∵点N在抛物线对称轴x=2上,
∴N(2,10+b),
∵AE2=OA2+0E2=26
∵MN=AE
∴MN2=AE2,
∴MN2=(2﹣1)2+[8﹣(10+b)]2=1+(b+2)2
∵M点的坐标为M1(1,8)或M2(3,8),
∴点M1,M2关于抛物线对称轴x=2对称,
∵点N在抛物线对称轴上,
∴M1N=M2N,
∴1+(b+2)2=26,
∴b=3,或b=﹣7,
∴10+b=13或10+b=3
∴当M点的坐标为(1,8)时,N点坐标为(2,13),
当M点的坐标为(3,8)时,N点坐标为(2,3)
【解析】(1)设出抛物线解析式,用待定系数法求解即可;(2)先求出直线AB解析式,设出点P坐标(x,﹣x2+4x+5),建立函数关系式S四边形APCD=﹣2x2+10x,根据二次函数求出极值;(3)先判断出△HMN≌△AOE,求出M点的横坐标,从而求出点M,N的坐标.此题是二次函数综合题,主要考查了待定系数法求函数关系式,函数极值的确定方法,平行四边形的性质和判定,解本题的关键是建立函数关系式求极值.
【考点精析】掌握二次函数的最值是解答本题的根本,需要知道如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a.