题目内容
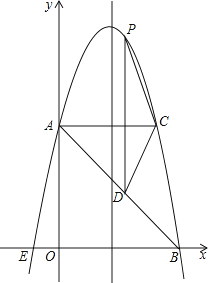
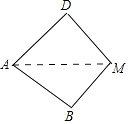
【题目】已知：如图1，图形①满足AD=AB，MD=MB，∠A=72°，∠M=144°．图形②与图形①恰好拼成一个菱形（如图2）．记AB的长度为a，BM的长度为b． 
（1）图形①中∠B=°，图形②中∠E=°；
（2）小明有两种纸片各若干张，其中一种纸片的形状及大小与图形①相同，这种纸片称为“风筝一号”；另一种纸片的形状及大小与图形②相同，这种纸片称为“飞镖一号”． ①小明仅用“风筝一号”纸片拼成一个边长为b的正十边形，需要这种纸片张；
【答案】
（1）72；36
（2）5 ②小明若用若干张“风筝一号”纸片和“飞镖一号”纸片拼成一个“大风筝”（如图3），其中∠P=72°，∠Q=144°，且PI=PJ=a+b，IQ=JQ．请你在图3中画出拼接线并保留画图痕迹．（本题中均为无重叠、无缝隙拼接）
根据题意可知：“风筝一号”纸片用两张和“飞镖一号”纸片用一张，
画出拼接线如图所示：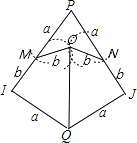
【解析】解：（1）连接AM，如图所示： ∵AD=AB，DM=BM，AM为公共边，
∴△ADM≌△ABM，
∴∠D=∠B，
又因为四边形ABMD的内角和等于360°，∠DAB=72°，∠DMB=144°，
∴∠B= 
=72°；
在图2中，因为四边形ABCD为菱形，所以AB∥CD，
∴∠A+∠ADC=∠A+∠ADM+∠CEF=180°，∠A=72°，∠ADM=72°，
∴∠CEF=180°﹣72°﹣72°=36°；
2）①用“风筝一号”纸片拼成一个边长为b的正十边形，
得到“风筝一号”纸片的点A与正十边形的中心重合，又∠A=72°，
则需要这种纸片的数量= 
=5；
②根据题意可知：“风筝一号”纸片用两张和“飞镖一号”纸片用一张，
画出拼接线如图所示：
所以答案是：（1）72°；36°；（2）①、5．
【考点精析】本题主要考查了菱形的性质和正多边形和圆的相关知识点，需要掌握菱形的四条边都相等；菱形的对角线互相垂直，并且每一条对角线平分一组对角；菱形被两条对角线分成四个全等的直角三角形；菱形的面积等于两条对角线长的积的一半；圆的内接四边形的对角互补，并且任何一个外角都等于它的内对角；圆的外切四边形的两组对边的和相等才能正确解答此题．
