Question

【题目】如图，E为正方形ABCD中CD边上一点，∠DAE=30°，P为AE的中点，过点P作直线分别与AD、BC相交于点M、N．若MN=AE，则∠AMN等于________

Answer 1

【答案】60°或120°

【解析】

画出符合的两种情况，过N作NF⊥AD于F，根据HL证出Rt△MFN≌Rt△EDA，即可求出答案．

分为两种情况：①如图1，

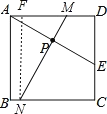
过N作NF⊥AD于F，

则∠NFA=∠MFN=90°，

∵四边形ABCD是正方形，

∴AD=AB,∠DAB=∠B=∠D=90°，

∴四边形AFNB是矩形，

∴NF=AB=AD，

∵∠NFM=∠D=90°，

在Rt△MFN和Rt△EDA中

∴Rt△MFN≌Rt△EDA(HL)，

∴∠AMN=∠AED，

∵∠DAE=30°,∠D=90°，

∴∠AMN=∠AED=180°30°90°=60°；

②如图2，

同法可求Rt△MFN≌Rt△EDA，

所以∠FMN=∠AED=60°，

所以∠AMN=180°60°=120°.

故答案为：60°或120°.