题目内容
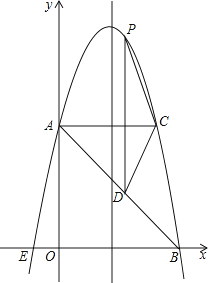
【题目】如图，点D、E分别为△ABC的边AB、AC上的中点，则△ADE的面积与四边形BCED的面积的比为（ ） 
A.1：2
B.1：3
C.1：4
D.1：1
【答案】B
【解析】解：∵D、E分别为△ABC的边AB、AC上的中点，
∴DE是△ABC的中位线，
∴DE∥BC，DE= 
BC，
∴△ADE∽△ABC，
∴△ADE的面积：△ABC的面积=（ ）2=1：4，
∴△ADE的面积：四边形BCED的面积=1：3；
故选：B．
证明DE是△ABC的中位线，由三角形中位线定理得出DE∥BC，DE= BC，证出△ADE∽△ABC，由相似三角形的性质得出△ADE的面积：△ABC的面积=1：4，即可得出结果．本题考查了相似三角形的判定与性质、三角形中位线定理；熟记三角形中位线定理，证明三角形相似是解决问题的关键．
练习册系列答案
相关题目
【题目】为了解中考考生最喜欢做哪种类型的英语客观题，2015年志愿者奔赴全市中考各考点对英语客观题的“听力部分、单项选择、完型填空、阅读理解、口语应用”进行了问卷调查，要求每位考生都自主选择其中一个类型，为此随机调查了各考点部分考生的意向．并将调查结果绘制成如图的统计图表（问卷回收率为100%，并均为有效问卷）．
被调查考生选择意向统计表
题型 | 所占百分比 |
听力部分 | a |
单项选择 | 35% |
完型填空 | b |
阅读理解 | 10% |
口语应用 | c |
根据统计图表中的信息，解答下列问题：
（1）求本次被调查的考生总人数及a、b、c的值；
（2）将条形统计图补充完整；
（3）全市参加这次中考的考生共有42000人，试估计全市考生中最喜欢做“单项选择”这类客观题的考生有多少人？
