Question

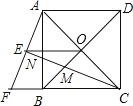
【题目】如图，矩形ABCD中，已知AB=6，BC=8，BD的垂直平分线交AD于点E，交BC于点F，则△BOF的面积为 ．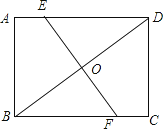

Answer 1

【答案】
【解析】解：∵四边形ABCD是矩形，
∴∠A=90°，又AB=6，AD=BC=8，
∴BD= =10，
∵EF是BD的垂直平分线，
∴OB=OD=5，∠BOF=90°，又∠C=90°，
∴△BOF∽△BCD，
∴ = ，即 = ，解得，BF= ，则OF= = ，则△BOF的面积= ×OF×OB= ，所以答案是： ．
【考点精析】关于本题考查的线段垂直平分线的性质和勾股定理的概念，需要了解垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线；线段垂直平分线的性质定理：线段垂直平分线上的点和这条线段两个端点的距离相等；直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能得出正确答案．