题目内容
【题目】已知,在△ABC中,∠BAC=90°,∠ABC=45°,点D为直线BC上一动点(点D不与点B,C重合).以AD为边作正方形ADEF,连接CF.
(1)如图1,当点D在线段BC上时.求证:CF+CD=BC;
(2)如图2,当点D在线段BC的延长线上时,其他条件不变,请直接写出CF,BC,CD三条线段之间的关系;
(3)如图3,当点D在线段BC的反向延长线上时,且点A,F分别在直线BC的两侧,其他条件不变;
①请直接写出CF,BC,CD三条线段之间的关系;
②若正方形ADEF的边长为2![]() ,对角线AE,DF相交于点O,连接OC.求OC的长度.
,对角线AE,DF相交于点O,连接OC.求OC的长度.

【答案】(1)证明见解析;(2)CF-CD=BC;(3)①CD-CF=BC;②2.
【解析】试题分析:(1)、根据正方形的性质判定出△BAD和△CAF全等,从而得出BD=CF,根据BD+CD=BC得出答案;(2)、根据图形得出线段之间的关系;(3)、首先根据正方形的性质证明△BAD和△CAF全等,然后得出∠ACF=∠ABD=135°,从而说明△FCD为直角三角形,根据正方形的对角线得出DF的长度,然后根据直角三角形斜边上的中线的性质得出OC的长度.
试题解析:(1)、∵∠BAC=90°,∠ABC=45°,∴∠ACB=∠ABC=45°,∴AB=AC,
∵四边形ADEF是正方形,∴AD=AF,∠DAF=90°,
∵∠BAD=90°-∠DAC,∠CAF=90°-∠DAC,∴∠BAD=∠CAF,
则在△BAD和△CAF中,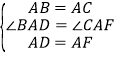 ∴△BAD ≌ △CAF(SAS),∴BD=CF,
∴△BAD ≌ △CAF(SAS),∴BD=CF,
∵BD+CD=BC,∴CF+CD=BC;
(2)、CF-CD=BC
(3)、①CD-CF =BC.
②∵∠BAC=90°,∠ABC=45°,∴∠ACB=∠ABC=45°,∴AB=AC, ∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°, ∵∠BAD=90°-∠BAF,∠CAF=90°-∠BAF,∴∠BAD=∠CAF,
则在△BAD和△CAF中,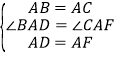 ∴△BAD ≌ △CAF(SAS),
∴△BAD ≌ △CAF(SAS),
∴∠ABD=∠ACF,∵∠ABC=45°,∠ABD=135°, ∴∠ACF=∠ABD=135°,
∴∠FCD=90°,∴△FCD是直角三角形. ∵正方形ADEF的边长为![]() 且对角线AE、DF相交于点O,
且对角线AE、DF相交于点O,
∴DF=![]() AD=4,O为DF中点. ∴OC=
AD=4,O为DF中点. ∴OC=![]() DF=2.
DF=2.

【题目】有这样一个问题:探究函数![]() 的图象与性质.小美根据学习函数的经验,对函数
的图象与性质.小美根据学习函数的经验,对函数![]() 的图象与性质进行了探究.下面是小美的探究过程,请补充完整:
的图象与性质进行了探究.下面是小美的探究过程,请补充完整:
(![]() )函数
)函数![]() 的自变量
的自变量![]() 的取值范围是__________.
的取值范围是__________.
(![]() )下表是
)下表是![]() 与
与![]() 的几组对应值.
的几组对应值.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
如图,在平面直角坐标系![]() 中,描出以上表中各对对应值为坐标的点.
中,描出以上表中各对对应值为坐标的点.
根据描出的点,画出该函数的图象,标出函数的解析式.

(![]() )结合函数的图象,写出该函数的一条性质:__________.
)结合函数的图象,写出该函数的一条性质:__________.