题目内容
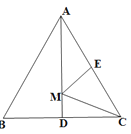
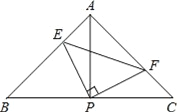
【题目】如图，在△ABC中，D是BC的中点，DE⊥AB于E，DF⊥AC于F，BE=CF．
（1）求证：AD平分∠BAC；
（2）连接EF，求证：AD垂直平分EF．
【答案】见解析
【解析】试题分析：（1）由于D是BC的中点，那么BD=CD，而BE=CF，DE⊥AB，DF⊥AC，利用HL易证
，可得DE=DF，利用角平分线的判定定理可知点点D在∠BAC的平分线上，即AD平分∠BAC；
（2）根据全等三角形的性质即可得到结论．
试题解析：
(1)∵D是BC的中点
∴BD=CD，
又∵BE=CF，DE⊥AB，DF⊥AC，
∴DE=DF，
∴点D在∠BAC的平分线上，
∴AD平分∠BAC；
(2) 
∴∠B=∠C，
∴AB=AC，
∵BE=CF，
∴ABBE=ACCF，
∴AE=AF，
∵DE=DF，
∴AD垂直平分EF.
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
【题目】某农产品店利用网络将优质土特产销往全国，其中销售的核桃和花生这两种商品的相关信息如下表：
商品 | 核桃 | 花生 |
规格 | 1 kg/袋 | 2 kg/袋 |
利润 | 10元/袋 | 8元/袋 |
根据上表提供的信息，解答下列问题：
（1）已知今年上半年，该店销售上表规格的核桃和花生共3000kg，获得利润21000元，求上半年该店销售这种规格的核桃和花生各多少袋；
（2）根据之前的销售情况，估计今年下半年，该店还能销售上表规格的核桃和花生共2000kg，其中，核桃的销售量不低于600kg．假设今年下半年，销售上表规格的核桃为
（kg），销售上表规格的核桃和花生获得的总利润为
（元），写出与之间的函数关系式，并求下半年该店销售这种规格的核桃和花生至少获得的总利润．
