题目内容
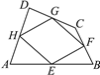
【题目】如图1,AB是⊙O的直径,点C在AB的延长线上,AB=4,BC=2,P是⊙O上半部分的一个动点,连接OP,CP.
(1)求△OPC的最大面积;
(2)求∠OCP的最大度数;
(3)如图2,延长PO交⊙O于点D,连接DB,当CP=DB时,求证:CP是⊙O的切线.
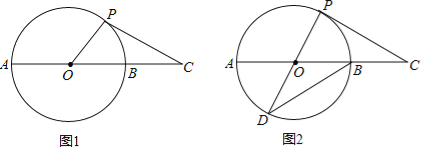
【答案】
【解析】
试题(1)在△OPC中,底边OC长度固定,因此要想△OPC的面积最大,则要OC边上的高最大;由图形可知,当OP⊥OC时高最大;
(2)要想∠OCP的度数最大,由图形可知当PC与⊙O相切才能满足,根据切线的性质即可求得;
(3)连接AP,BP通过△ODB≌△BPC可求得DP⊥PC,从而求得PC是⊙O的切线
试题解析:(1)∵AB=4,
∴OB=2,OC=OB+BC=4.
在△OPC中,设OC边上的高为h,
∵S△OPC=![]() OCh=2h,
OCh=2h,
∴当h最大时,S△OPC取得最大值.
观察图形,当OP⊥OC时,h最大,如答图1所示:
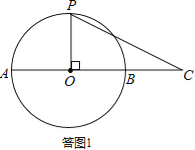
此时h=半径=2,S△OPC=2×2=4.
∴△OPC的最大面积为4.
(2)当PC与⊙O相切时,∠OCP最大.如答图2所示:
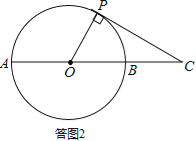
∵tan∠OCP=![]() ,
,
∴∠OCP=30°
∴∠OCP的最大度数为30°.
(3)证明:如答图3,连接AP,BP.
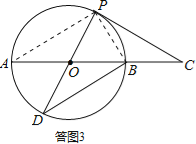
∴∠A=∠D=∠APD=∠ABD,
∵∠AOP=∠DOB
∴AP=BD,
∵CP=DB,
∴AP=CP,
∴∠A=∠C
∴∠A=∠D=∠APD=∠ABD∠C,
在△ODB与△BPC中
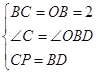 ,
,
∴△ODB≌△BPC(SAS),
∴∠D=∠BPC,
∵PD是直径,
∴∠DBP=90°,
∴∠D+∠BPD=90°,
∴∠BPC+∠BPD=90°,
∴DP⊥PC,
∵DP经过圆心,
∴PC是⊙O的切线.

【题目】某校九年级两个班,各选派10名学生参加学校举行的“汉字听写”大赛预赛.各参赛选手的成绩如图:
九(1)班:88,91,92,93,93,93,94,98,98,100
九(2)班:89,93,93,93,95,96,96,98,98,99
通过整理,得到数据分析表如下:
班级 | 最高分 | 平均分 | 中位数 | 众数 | 方差 |
九(1)班 | 100 | m | 93 | 93 | 12 |
九(2)班 | 99 | 95 | n | 93 | 8.4 |
(1)直接写出表中m、n的值;
(2)依据数据分析表,有人说:“最高分在(1)班,(1)班的成绩比(2)班好”,但也有人说(2)班的成绩要好,请给出两条支持九(2)班成绩好的理由;
(3)若从两班的参赛选手中选四名同学参加决赛,其中两个班的第一名直接进入决赛,另外两个名额在四个“98分”的学生中任选二个,试求另外两个决赛名额落在同一个班的概率.