题目内容
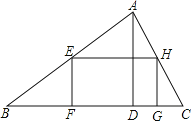
【题目】如图,在△ABC中,AD是BC上的高,且BC=9,AD=3,矩形EFGH的顶点F、G在边BC上,顶点E、H分别在边AB和AC上,如果设边EF的长为x(0<x<3),矩形EFGH的面积为y,那么y关于x的函数解析式是_____.
【答案】y=﹣3x2+9x(0<x<3).
【解析】
根据矩形性质得:EH∥BC,从而得△AEH∽△ABC,利用相似三角形对应边的比和对应高的比相等表示EH的长,利用矩形面积公式得y与x的函数解析式.
解:∵四边形EFGH是矩形,
∴EH∥BC,
∴△AEH∽△ABC,
∴![]()
∵EF=DM=x,AD=3,
∴AM=3﹣x,
∴![]()
∴EH=3(3﹣x)=9﹣3x,
∴y=EHEF=x(9﹣3x)=﹣3x2+9x(0<x<3).
故答案为:y=﹣3x2+9x(0<x<3).


练习册系列答案
相关题目