Question

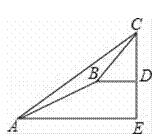
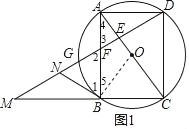
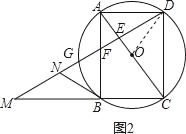
【题目】如图，四边形ABCD为⊙O的内接四边形，且对角线AC为直径，AD＝BC，过点D作DG⊥AC，垂足为E，DG分别与AB，⊙O及CB延长线交于点F、G、M．

（1）求证：四边形ABCD为矩形；

（2）若N为MF中点，求证：NB是⊙O的切线；

（3）若F为GE中点，且DE＝6，求⊙O的半径．

Answer 1

【答案】（1）详见解析；（2）详见解析；（3）⊙O的半径是．

【解析】

（1）根据AC为⊙O直径，得到∠ADC＝∠CBA＝90°，通过全等三角形得到CD＝AB，推出四边形ABCD是平行四边形，根据矩形的判定定理得到结论；

（2）根据直角三角形的性质得到NB＝MF＝NF，根据等腰三角形的性质和余角的性质即可得到NB是⊙O的切线；

（3）根据垂径定理得到DE＝GE＝6，根据四边形ABCD是矩形，得到∠BAD＝90°，根据余角的性质得到∠FAE＝∠ADE，推出△AEF∽△DEA，根据相似三角形的性质列比例式得到AE＝3，连接OD，设⊙O的半径为r，根据勾股定理列方程即可得到结论．

解：（1）∵AC为⊙O直径，

∴∠ADC＝∠CBA＝90°，

在Rt△ADC与Rt△CBA中，，

∴Rt△ADC≌Rt△CBA，

∴CD＝AB，

∵AD＝BC，

∴四边形ABCD是平行四边形，

∵∠CBA＝90°，

∴四边形ABCD是矩形；

（2）连接OB，

∵∠MBF＝∠ABC＝90°，

∴NB＝MF＝NF，

∴∠1＝∠2，

∵∠2＝∠3，

∴∠1＝∠3，

∵OB＝OA，

∴∠5＝∠4，

∵DG⊥AC，

∴∠AEF＝90°，

∴∠3+∠4＝90°，

∴∠1+∠5＝90°，

∴OB⊥NB，

∴NB是⊙O的切线；

（3）∵AC为⊙O直径，AC⊥DG，

∴DE＝GE＝6，

∵F为GE中点，

∴EF＝GF＝3，

∵四边形ABCD是矩形，

∴∠BAD＝90°，

∴∠FAE+∠DAE＝90°，

∵∠ADE+∠DAE＝90°，

∴∠FAE＝∠ADE，

∵∠AEF＝∠DEA＝90°，

∴△AEF∽△DEA，

∴，

∴AE＝3，

连接OD，设⊙O的半径为r，

∴OA＝OD＝r，OE＝r﹣3，

∵OE2+DE2＝OD2，

∴（r﹣3）2+62＝r2，

∴r＝，

∴⊙O的半径是．