题目内容
推理证明(本小题满分6分)
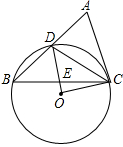
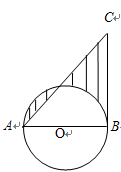
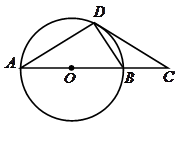
如图,在△ABC中,D是AB边上一点,圆O过D、B、C三点, ÐDOC=2ÐACD=90°.
(1)求证:直线AC是圆O的切线;
(2)如果ÐACB=75°,圆O的半径为2,求BD的长.
如图,在△ABC中,D是AB边上一点,圆O过D、B、C三点, ÐDOC=2ÐACD=90°.

(1)求证:直线AC是圆O的切线;
(2)如果ÐACB=75°,圆O的半径为2,求BD的长.
(1)见解析(2)4
(1)证明:
∵2∠ACD=90°,
∴∠ACD=45°
∵∠DOC=90°,且DO=CO,
∴△OCD为等腰直角三角形,∠OCD=45°
∴∠ACO=∠ACD+∠DCO=45°+45°=90°
∴直线AC是⊙O的切线.
(2)解:连接BO,
∵∠ACB=75°,∠ACD=45°,
∴∠DCB=30°,∴∠DOB=60°,
∵DO=BO,
∴△BDO为等边三角形,
∴BD=OB=4.
(1)利用切线的判定定理求出∠ACO=∠ACD+∠DCO=45°+45°=90°,即可得出答案;
(2)利用圆周角定理得出△BDO为等边三角形,即可得出答案.
∵2∠ACD=90°,
∴∠ACD=45°
∵∠DOC=90°,且DO=CO,
∴△OCD为等腰直角三角形,∠OCD=45°
∴∠ACO=∠ACD+∠DCO=45°+45°=90°
∴直线AC是⊙O的切线.
(2)解:连接BO,
∵∠ACB=75°,∠ACD=45°,
∴∠DCB=30°,∴∠DOB=60°,
∵DO=BO,
∴△BDO为等边三角形,
∴BD=OB=4.
(1)利用切线的判定定理求出∠ACO=∠ACD+∠DCO=45°+45°=90°,即可得出答案;
(2)利用圆周角定理得出△BDO为等边三角形,即可得出答案.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
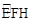 上异于E、H的点.若∠A=50°,则∠EPH= .
上异于E、H的点.若∠A=50°,则∠EPH= .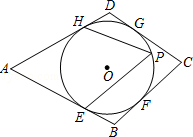
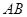 是⊙O的直径,
是⊙O的直径,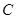 为
为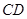 交⊙O于点
交⊙O于点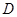 ,且
,且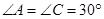 .
. 
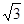 :2,求⊙O的半径及弦DF的长
:2,求⊙O的半径及弦DF的长