题目内容
如图,圆周角∠BAC=55°,分别过B,C两点作⊙O的切线,两切线相交与点P,则∠BPC= ▲ °.

70。
切线的性质,圆周角定理。
连接OB,OC,
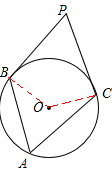
∵PB,PC是⊙O的切线,∴OB⊥PB,OC⊥PC。
∴∠PBO=∠PCO=90°,
∵∠BOC=2∠BAC=2×55°=110°,
∴∠BPC=360°-∠PBO-∠BOC-∠PCO=360°-90°-110°-90°=70°。
连接OB,OC,

∵PB,PC是⊙O的切线,∴OB⊥PB,OC⊥PC。
∴∠PBO=∠PCO=90°,
∵∠BOC=2∠BAC=2×55°=110°,
∴∠BPC=360°-∠PBO-∠BOC-∠PCO=360°-90°-110°-90°=70°。

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
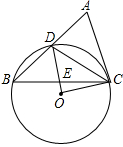
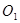 的半径为5
的半径为5 ,⊙
,⊙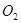 的半径为3
的半径为3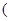
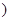
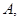 外离
外离 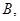 外切
外切 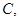 内切
内切 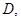 相交
相交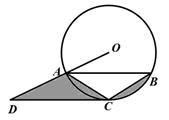
 )
)
 ▲ ;
▲ ;