题目内容
【题目】如图,在△ABC中,AC=4,BC=2,点D是边AB上一点,CD将△ABC分成△ACD和△BCD,若△ACD是以AC为底的等腰三角形,且△BCD与△BAC相似,则CD的长为( )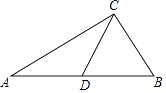
A.![]()
B.2
C.4 ![]() ﹣4
﹣4
D.![]()
【答案】D
【解析】∵△ACD是以AC为底的等腰三角形,
∴AD=CD,
∵△BCD与△BAC相似,
∴ ![]() =
= ![]() ,
,
设CD=x,BD=y,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴ ![]() ,
,
解得:x=2y,
∴y= ![]() ,
,
∴x= ![]() ,
,
∴CD= ![]() ,
,
所以答案是:D.
【考点精析】本题主要考查了等腰三角形的性质和相似三角形的性质的相关知识点,需要掌握等腰三角形的两个底角相等(简称:等边对等角);对应角相等,对应边成比例的两个三角形叫做相似三角形才能正确解答此题.

练习册系列答案
相关题目