题目内容
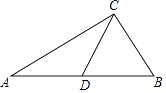
【题目】已知:在直角梯形ABCD中,AD∥BC,∠C=90°,AB=AD=25,BC=32.连接BD,AE⊥BD垂足为E.
(1)求证:△ABE∽△DBC;
(2)求线段AE的长.
【答案】
(1)证明:∵AB=AD=25,
∴∠ABD=∠ADB,
∵AD∥BC,
∴∠ADB=∠DBC,
∴∠ABD=∠DBC,
∵AE⊥BD,
∴∠AEB=∠C=90°,
∴△ABE∽△DBC
(2)解:∵AB=AD,又AE⊥BD,
∴BE=DE,
∴BD=2BE,
由△ABE∽△DBC,
得 ![]() ,
,
∵AB=AD=25,BC=32,
∴ ![]() ,
,
∴BE=20,
∴AE= ![]() .
.
【解析】(1)利用平行线和等腰三角形性质可推出两角对应相等,进而推出两三角形相似;(2)由三角形相似△ABE∽△DBC推出对应边成比例先求BE,再利用勾股定理求出AE.
【考点精析】利用勾股定理的概念和直角梯形对题目进行判断即可得到答案,需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;一腰垂直于底的梯形是直角梯形.

练习册系列答案
相关题目