题目内容
【题目】如图,一次函数y=kx+b与反比例函数y= ![]() (x>0)的图象交于A(m,6),B(3,n)两点
(x>0)的图象交于A(m,6),B(3,n)两点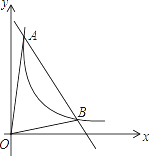
(1)求一次函数的解析式;
(2)根据图象直接写出使kx+b< ![]() 成立的x的取值范围;
成立的x的取值范围;
(3)求△AOB的面积.
【答案】
(1)解:∵点A(m,6),B(3,n)两点在反比例函数y= ![]() (x>0)的图象上,
(x>0)的图象上,
∴m=1,n=2, 即A(1,6),B(3,2). 又∵点A(m,6),B(3,n)两点在一次函数y=kx+b的图象上,
∴ ![]() . 解得
. 解得 ![]() ,
,
则该一次函数的解析式为:y=﹣2x+3
(2)解:根据图象可知使kx+b< ![]() 成立的x的取值范围是0<x<1或x>2;
成立的x的取值范围是0<x<1或x>2;
(3)解:分别过点A、B作AE⊥x轴,BC⊥x轴,垂足分别是E、C点.直线AB交x轴于D点.
令﹣2x+8=0,得x=4,即D(4,0).
∵A(1,6),B(3,2), 则 ![]() =4×6÷2-4×2÷2=12-4=8
=4×6÷2-4×2÷2=12-4=8
【解析】 (1)先将点A、B的坐标分别代入反比例函数解析式求出这两点坐标,再利用待定系数法,求出一次函数的解析式。
(2)要求一次函数值小于反比例函数值,要看直线x=1,直线x=3,两条直线将两函数分成三部分,这三部分的自变量的取值范围分别是0<x<1、x>3.1<<3,即可观察一次函数图象在反比例函数图象下方时所对应的x的取值范围。
(3)添加辅助线,分别过点A、B作AE⊥x轴,BC⊥x轴,垂足分别是E、C点.直线AB交x轴于D点。先求出点D的坐标,然后根据![]() ,即可求出结果。或过点A作AE⊥x轴,交OB于点H,△OAB的面积=△OAH的面积+△HAB的面积.
,即可求出结果。或过点A作AE⊥x轴,交OB于点H,△OAB的面积=△OAH的面积+△HAB的面积.
【考点精析】掌握确定一次函数的表达式和反比例函数的性质是解答本题的根本,需要知道确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大.

【题目】抗震救灾中,某县粮食局为了保证库存粮食的安全,决定将甲、乙两个仓库的粮食,全部转移到具有较强抗震功能的A、B两仓库.已知甲库有粮食100吨,乙库有粮食80吨,而A库的容量为70吨,B库的容量为110吨.从甲、乙两库到A、B两库的路程和运费如下表:(表中“元/吨千米”表示每吨粮食运送1千米所需人民币)
路程(千米) | 运费(元/吨千米) | |||
甲库 | 乙库 | 甲库 | 乙库 | |
A库 | 20 | 15 | 12 | 12 |
B库 | 25 | 20 | 10 | 8 |
(1)若甲库运往A库粮食x吨,请写出将粮食运往A、B两库的总运费y(元)与x(吨)的函数关系式;
(2)当甲、乙两库各运往A、B两库多少吨粮食时,总运费最省,最省的总运费是多少?