题目内容
【题目】综合题
(1)【问题提出】如图1.△ABC是等边三角形,点D在线段AB上.点E在直线BC上.且∠DEC=∠DCE.求证:BE=AD;
(2)【类比学习】如图2.将条件“点D在线段AB上”改为“点D在线段AB的延长线上”,其他条件不变.判断线段AB,BE,BD之间的数量关系,并说明理由.
(3)【扩展探究】如图3.△ABC是等腰三角形,AB=AC,∠BAC=120°,点D在线段AB的反向延长线上,点E在直线BC上,且∠DEC=∠DCE,【类比学习】中的线段AB、BE、BD之间的数量关系是否还成立?若成立,请说明理由;若不成立,请直接写出线段AB,BE,BD之间的数量.
【答案】
(1)证明:作DF∥BC交AC于F,如图1所示:
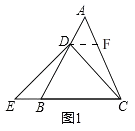
则∠ADF=∠ABC,∠AFD=∠ACB,∠FDC=∠DCE,
∵△ABC是等腰三角形,∠A=60°,
∴△ABC是等边三角形,
∴∠ABC=∠ACB=60°,
∴∠DBE=120°,∠ADF=∠AFD=60°=∠A,
∴△ADF是等边三角形,∠DFC=120°,
∴AD=DF,
∵∠DEC=∠DCE,
∴∠FDC=∠DEC,ED=CD,
在△DBE和△CFD中, 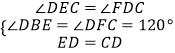 ,
,
∴△DBE≌△CFD(AAS),
∴EB=DF,
∴EB=AD
(2)解:EB=AB+BD;理由如下:
作DF∥BC交AC的延长线于F,如图2所示:
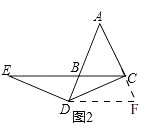
同(1)得:AD=DF,∠FDC=∠ECD,∠FDC=∠DEC,ED=CD,
又∵∠DBE=∠DFC=60°,
∴在△DBE和△CFD中, 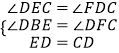 ,
,
∴△DBE≌△CFD(AAS),
∴EB=DF,
∴EB=AD,
∴EB=AB+BD
(3)解: ![]() BE=3DB﹣3AB.
BE=3DB﹣3AB.
理由:作DF∥BC交CA的延长线于F,如图3所示,
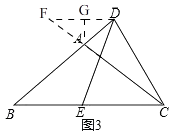
则∠ADF=∠ABC,∠AFD=∠ACB,∠FDC+∠DCE=180°,
∵△ABC是等腰三角形,
∴∠ABC=∠ACB,
∴∠ADF=∠AFD=∠ABC,
∵∠DEC=∠DCE,
∴DE=DC,∠FDC+∠DEC=180°,
∵∠DEC+∠DEB=180°,
∴∠FDC=∠DEB,
在△DBE和△CFD中, 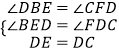 ,
,
∴△DBE≌△CFD(AAS),
∴EB=DF,DB=CF,
∵CF=AC+AF=AB+AF,
∴DB=AB+AF,
过点A作AG⊥DF于G,
∵AF=AD,
∴DF=2FG,
在Rt△AFG中,∠AFG=90°﹣∠FAG=90°﹣ ![]() ∠BAC=30°,
∠BAC=30°,
∴FG= ![]() AF,
AF,
∴EB=DF=2FG= ![]() AF,
AF,
∴AF= ![]() EB
EB
∴DB=AB+ ![]() BE,
BE,
即: ![]() BE=3DB﹣3AB.
BE=3DB﹣3AB.
【解析】(1)作DF∥BC交AC于F,首先证明△ABC是等边三角形,然后再由AAS证明△DBE≌△CFD,得出EB=DF,即可得出结论;
(2)作DF∥BC交AC的延长线于F,首先证明△DBE≌△CFD,从而可得到EB=DF,即可得出结论;
(3)作DF∥BC交CA的延长线于F,首先证明△DBE≌△CFD,从而可得到EB=DF,再利用含30°的直角三角形的性质即可得出结论.