Question

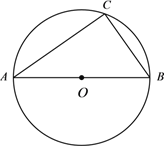
【题目】如图，已知在⊙O中，AB是⊙O的直径，AC＝8，BC＝6．

（1）求⊙O的面积；

（2）若D为⊙O上一点，且△ABD为等腰三角形，求CD的长.

Answer 1

【答案】（1）25π；（2）CD1＝，CD2＝7

【解析】分析：（1）利用圆周角定理的推论得到∠C是直角，利用勾股定理求出直径AB，再利用圆的面积公式即可得到答案；

（2）分点D在上半圆中点与点D在下半圆中点这两种情况进行计算即可.

详解：（1）∵AB是⊙O的直径，

∴∠ACB=90°，

∵AB是⊙O的直径，

∴AC＝8，BC＝6，

∴AB＝10，

∴⊙O的面积＝π×52＝25π．

（2）有两种情况：

①如图所示，当点D位于上半圆中点D1时，可知△ABD1是等腰直角三角形，且OD1⊥AB,

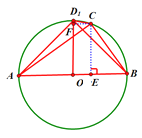
作CE⊥AB垂足为E，CF⊥OD1垂足为F，可得矩形CEOF，

∵CE＝，

∴OF= CE=，

∴，

∵=,

∴，

∴，

∴；

②如图所示，当点D位于下半圆中点D2时，

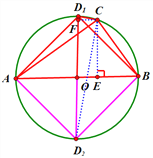
同理可求.

∴CD1＝，CD2＝7