题目内容
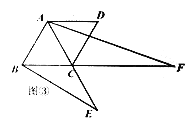
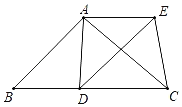
【题目】如图,在△ABC中,AB=AC,点D在边BC上,联结AD,以AD为一边作△ADE,满足AD=AE,∠DAE=∠BAC,联结EC.
(1)求证:CA平分∠DCE;
(2)如果AB2=BDBC,求证:四边形ABDE是平行四边形.
【答案】(1)见解析;(2)见解析
【解析】
(1)根据等腰三角形的性质得到∠B=∠ACB,证明△ABD≌△ACE,根据全等三角形的性质得到∠B=∠ACE,根据角平分线的定义证明结论;
(2)根据相似三角形的判定定理得到△ABD∽△CBA,得到∠BAD=∠ACB,分别证明AE∥BD,AB∥DE,根据平行四边形的判定定理证明.
(1)证明:∵AB=AC,
∴∠B=∠ACB,
∵∠DAE=∠BAC,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,即∠BAD=∠CAE,
在△ABD和△ACE中,
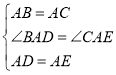 ,
,
∴△ABD≌△ACE(SAS),
∴∠B=∠ACE,
∴∠ACB=∠ACE,
∴CA平分∠DCE;
(2)证明:∵AB2=BDBC,
∴![]() =
=![]() ,
,
又∠B=∠B,
∴△ABD∽△CBA,
∴∠BAD=∠ACB,
∵△ABD≌△ACE,
∴∠BAD=∠CAE,
∴∠CAE=∠ACB,
∴AE∥BD,
∵AB=AC,AD=AE,∠DAE=∠BAC,
∴∠ACB=∠ADE,
∴∠BAD=∠ADE,
∴AB∥DE,
∵AE∥BD,AB∥DE,
∴四边形ABDE是平行四边形.

练习册系列答案
相关题目