题目内容
【题目】为了贯彻教育部关于中小学生“每天锻炼一小时”的要求,某市教育局做了一次随机抽样调查,其内容是:(1)学生每天锻炼时间是否达到1小时;(2)学生每天锻炼时间未达到1小时的原因.随机调查了600名学生,把所得的数据制成了如下的扇形统计图和条形统计图(不完整)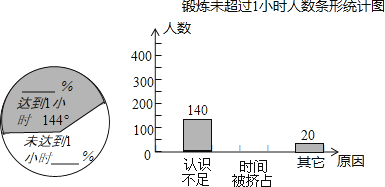
根据图示,回答以下问题:
(1)每天锻炼时间达到1小时的人数占被调查总人数的百分比是;
每天锻炼时间未达到1小时的人数占被调查总人数的百分比是;
每天锻炼时间未达到1小时的人数为人,其中原因是“时间被挤占”的人数是人;
(2)补全扇形统计图和条形统计图;
(3)若该市现有中小学生约27万人,据此调查,可估计今年该市中小学生每天锻炼未达到1小时的学生约有多少万人?
(4)从这次接受调查的学生中,随机抽取一名学生的“每天锻炼一小时”的情况,回答内容为“时间被挤占”的概率是多少?
【答案】
(1)40%;60%;360;200
(2)
解:补全统计图如图
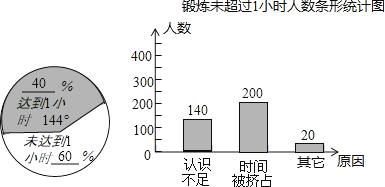
(3)
解:27×60%=16.2万人
(4)
解:P(时间被挤占)= 200 600 = 1 3 .
【解析】解:(1)达到1小时的人数占被调查总人数的百分比: ![]() ×100°=40%,
×100°=40%,
未达到1小时的人数占被调查总人数的百分比:1﹣40%=60%,
未达到1小时的人数:600×60%=360人,其中原因是“时间被挤占”的人数:360﹣140﹣20=200人;
所以答案是:40%,60%,360,200;
(1)用144°除以360°计算即可求出达到1小时的人数的百分比;
根据两部分所占的百分比之和为1计算即可求出未达到1小时的人数所占的百分比;
用所求的百分比乘以600,计算即可求出未达到1小时的人数,再根据条形统计图求出时间被挤占的人数;(2)根据(1)的计算补全统计图即可;(3)用总人数27万乘以“未达到1小时的学生”所占的百分比,计算即可得解;(4)用回答时间被挤占的人数除以接受调查的人数,计算即可得解.
【考点精析】认真审题,首先需要了解扇形统计图(能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况),还要掌握条形统计图(能清楚地表示出每个项目的具体数目,但是不能清楚地表示出各个部分在总体中所占的百分比以及事物的变化情况)的相关知识才是答题的关键.

 阅读快车系列答案
阅读快车系列答案【题目】福鼎市南溪水库的警戒水位是![]() ,以下是南溪水库管理处七月份某周监测到的水位变化情况,上周末恰好达到警戒水位(正数表示比前一天水位高,负数表示比前一天水位低).
,以下是南溪水库管理处七月份某周监测到的水位变化情况,上周末恰好达到警戒水位(正数表示比前一天水位高,负数表示比前一天水位低).
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
水位变化 |
|
|
|
|
|
|
|

![]() 星期四的水位是多少?
星期四的水位是多少?
![]() 从这周一到周日哪天的水位是最高的?
从这周一到周日哪天的水位是最高的?
![]() 以警戒水位为零点,用折线图表表示本周水位情况.
以警戒水位为零点,用折线图表表示本周水位情况.