��Ŀ����
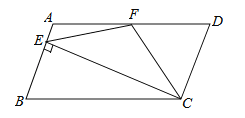
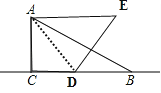
����Ŀ����ͼ����Rt��ABC�У���ACB=90�㣬��ABC=30�㣮��D��ֱ��BC�ϵ�һ�����㣬����AD������ADΪ����AD���Ҳ����ȱߡ�ADE��
��1����ͼ�٣�����Eǡ�����߶�BC��ʱ�����ж��߶�DE��BE��������ϵ�������ͼ��֤����Ľ��ۣ�
��2������E����ֱ��BC��ʱ������BE�������������䣬��1���н����Ƿ������������������ͼ�ڸ���֤����������������ֱ��д���µĽ��ۣ�
��3����AC=3����D��ֱ��BC���ƶ��Ĺ����У��Ƿ������A��C��D��EΪ������ı��������Σ�������ڣ�ֱ��д���߶�CD�ij��ȣ���������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺DE=BE���������£�
�ߡ�ADEΪ�ȱ������Σ�
��AD=DE=AE����AED=60�㣮
�ߡ�ABC=30�㣬��AED=��ABC+��EAB��
���EAB=60�㩁30��=30�㣬
���ABC=��EAB��
��EB=AE��
��EB=DE��
��2��
�⣺��ͼ��
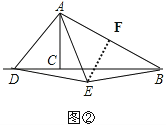
����E��EF��AB������ΪF��
�ڡ�ABC�У���ABC=30�㣬
���CAB=60�㣬
���DAE=��CAB��
���DAE����CAE=��BAC����CAE��
���CAD=��EAF��
�֡�AD=AE����ACD=��AFE��
���ADC�ա�AEF��
��AC=AF��
�ڡ�ABC�У���ABC=30�㣬
��AC= ![]() AB��
AB��
��AF=BF��
��EA=EB��
��DE=EB��
��3��
�⣺��ͼ��
���ı���ACDE�����Σ���ACD=90�㣬
���CAE=90�㣮
�ߡ�CAE=��CAD+��EAD��
�֡�����������ADE�У���EAD=60�㣬
���CAD=30�㣮
��ֱ��������ACD�У�AC=3����CAD=30�㣬
�ɹ��ɶ����ɵ�CD= ![]() ��
��
ͬ���ɵã�����D���B�غϣ�ACƽ��DE����ʱCD=3 ![]() ��
��
������������AE��CD��CD= ![]() ������D���B�غϣ���ʱCD=3
������D���B�غϣ���ʱCD=3 ![]()
����������1�����õȱ������ε������Լ����������ε��ж���ɣ���2������E��EF��AB������ΪF��֤�á�ADC�ա�AEF�����ֱ����������30�ȵĽ����Ե�ֱ�DZ���б�ߵ�һ�������⣻��3����A��C��D��EΪ��������ε��������֣����ҳ��������ķ�����
�����㾫�����������⣬������Ҫ�˽�ȱ������ε�����(�ȱ������ε������Ƕ���Ȳ���ÿ���Ƕ���60��)����Ҫ���պ�30�Ƚǵ�ֱ��������(��ֱ���������У����һ����ǵ���30�㣬��ô�����Ե�ֱ�DZߵ���б�ߵ�һ��)�����֪ʶ���Ǵ���Ĺؼ���

 ��У����ϵ�д�
��У����ϵ�д�����Ŀ����������Ϫˮ��ľ���ˮλ��![]() ����������Ϫˮ����������·�ij�ܼ���ˮλ�仯���������ĩǡ�ôﵽ����ˮλ��������ʾ��ǰһ��ˮλ�ߣ�������ʾ��ǰһ��ˮλ�ͣ���
����������Ϫˮ����������·�ij�ܼ���ˮλ�仯���������ĩǡ�ôﵽ����ˮλ��������ʾ��ǰһ��ˮλ�ߣ�������ʾ��ǰһ��ˮλ�ͣ���
���� | һ | �� | �� | �� | �� | �� | �� |
ˮλ�仯 |
|
|
|
|
|
|
|

![]() �����ĵ�ˮλ�Ƕ��٣�
�����ĵ�ˮλ�Ƕ��٣�
![]() ������һ�����������ˮλ����ߵģ�
������һ�����������ˮλ����ߵģ�
![]() �Ծ���ˮλΪ��㣬������ͼ����ʾ����ˮλ�����
�Ծ���ˮλΪ��㣬������ͼ����ʾ����ˮλ�����