题目内容
【题目】如图，在平面直角坐标系中， 
为坐标原点，点
在反比例函数
的图象上，作
轴于
点．
（1）
的面积为______；
（2）若点
的横坐标为4，点
在
轴的正半轴，且
是等腰三角形，求点
的坐标；
（3）动点
从原点出发，沿
轴的正方向运动，以
为直角边，在
的右侧作等腰
， 
；若在点
运动过程中，斜边
始终在
轴上，求 
的值．
【答案】6
【解析】分析: （1）首先过点B作BC⊥x轴于点C，由等腰三角形的三线合一，可得OC=AC=3，然后由顶点B在反比例函数
的图象上，求得点B的坐标；
（2）首先由等腰直角三角形的性质，可得OC=BC，然后由顶点B在反比例函数
的图象上，求得点B的坐标，继而求得点A的坐标；
（3）首先过点P作PD⊥x轴于点D，易得AD=PD，则可设AD=b，则点P（4
+b，b），又由点P在反比例函数
的图象上，求得b的值，继而求得答案．
详解:
（1） 6
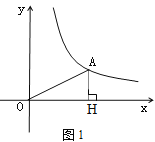
（2）依题意，得A（4，3），如图1，过A作AH⊥x轴于H，
∴AH=3，OH=4， 
；
要使△OAP是等腰三角形，有如下三种情况：
①当OP=OA时，OP=5
∴点P的坐标为（5，0）
②当AO=AP时，OP=2OH=8
∴点P的坐标为（8，0）
③当PO=PA时，如图2，设点P的横坐标为
，
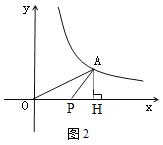
则PO=PA= 
，PH=
在Rt△AHP中， 
∴
解得： 
∴点P的坐标为（
，0）
综上所述，点P的坐标为（5，0）或 （8，0） 或（
，0）
（3）如图3，
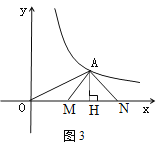
在等腰Rt△MAN，
∵AH⊥x轴于H
∴MH=AH=HN
∴ ON2－OM2=（ON+OM)(ON-OM)
=[（OH+HN)+(OH-MH)][(OH+HN)-(OH-MH)]
=(2OH)(HN+MH)
=(2OH)(2AH)
=4OH 
AH
4x12 =48
点睛: 本题考查了反比例函数的应用，现实生活中存在大量成反比例函数的两个变量，解答该类问题的关键是确定两个变量之间的函数关系，然后利用待定系数法求出它们的关系式．
