题目内容
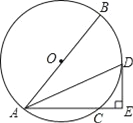
【题目】如图,OA、OB、OC都是⊙O的半径,∠AOB=2∠BOC,
(1)求证:∠ACB=2∠BAC;
(2)若AC平分∠OAB,求∠AOC的度数.

【答案】(1)证明详见解析;(2)135°.
【解析】
试题分析:(1)根据圆周角定理可得∠BOC=2∠BAC,∠AOB=2∠ACB,再根据条件∠AOB=2∠BOC可得∠ACB=2∠BAC;
(2)设∠BAC=x°,则∠OAB=2∠BAC=2x°,再表示出∠AOB=2∠ACB=4∠BAC=4x°,再根据三角形内角和为180°可得方程4x+2x+2x=180,再解即可得x的值,进而可得答案.
试题解析:(1)在⊙O中,∵∠AOB=2∠ACB,∠BOC=2∠BAC,
∵∠AOB=2∠BOC.
∴∠ACB=2∠BAC;
(2)解:设∠BAC=x°.
∵AC平分∠OAB,
∴∠OAB=2∠BAC=2x°,
∵∠AOB=2∠ACB,∠ACB=2∠BAC,
∴∠AOB=2∠ACB=4∠BAC=4x°,
在△OAB中,
∠AOB+∠OAB+∠OBA=180°,
∴4x+2x+2x=180,
解得:x=22.5,
∴∠AOC=6x°=135°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目