题目内容
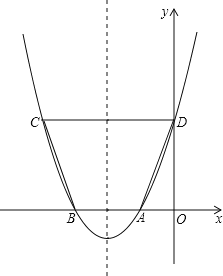
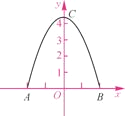
【题目】某工厂大门是一抛物线水泥建筑物(如图),大门地面宽AB=4 m,顶部C离地面高为4.4 m.
(1)以AB所在直线为x轴,抛物线的对称轴为y轴,建立平面直角坐标系,求该抛物线对应的函数表达式;
(2)现有一辆载满货物的汽车欲通过大门,货物顶点距地面2.8 m,装货宽度为2.4 m,请通过计算,判断这辆汽车能否顺利通过大门.
【答案】(1)y=-1.1x2+4.4.(2)这辆汽车能够通过大门.
【解析】
先过AB的中点作AB的垂直平分线建立直角坐标系,得出点A、B、C的坐标,用待定系数法即可求出过此三点的抛物线解析式,判断点(-1.2,2.8)或点(1.2,2.8)与抛物线的关系即可.
解:(1)如图,过AB的中点作AB的垂直平分线,建立平面直角坐标系.点A,B,C的坐标分别为 A(-2,0),B(2,0),C(0,4.4).
设抛物线的表达式为y=a(x-2)(x+2).
将点C(0,4.4)代入得
a(0-2)(0+2)=4.4,解得a=-1.1,
∴y=-1.1(x-2)(x+2)=-1.1x2+4.4.
故此抛物线的表达式为y=-1.1x2+4.4.
(2)∵货物顶点距地面2.8 m,装货宽度为2.4,
∴只要判断点(-1.2,2.8)或点(1.2,2.8)与抛物线的位置关系即可.
将x=1.2代入抛物线,得 y=2.816>2.8,
∴点(-1.2,2.8)和点(1.2,2.8)都在抛物线内.
∴这辆汽车能够通过大门.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目