题目内容
【题目】如图,A(-5,0),B(-3,0),点C在y轴的正半轴上,∠CBO=45°,CD∥AB.∠CDA=90°.点P从点Q(4,0)出发,沿x轴向左以每秒1个单位长度的速度运动,运动时时间t秒.

(1)求点C的坐标;
(2)当∠BCP=15°时,求t的值;
(3)以点P为圆心,PC为半径的⊙P随点P的运动而变化,当⊙P与四边形ABCD的边(或边所在的直线)相切时,求t的值.
【答案】(1)点C的坐标为(0,3);(2)t的值为4+![]() 或4+3
或4+3![]() ;(3)t=1或4或5.6
;(3)t=1或4或5.6
【解析】试题分析:(1)由∠CBO=45°,∠BOC为直角,得到△BOC为等腰直角三角形,又OB=3,利用等腰直角三角形AOB的性质知OC=OB=3,然后由点C在y轴的正半轴可以确定点C的坐标;
(2)需要对点P的位置进行分类讨论:①当点P在点B右侧时,如图2所示,由∠BCO=45°,用∠BCO-∠BCP求出∠PCO为30°,又OC=3,在Rt△POC中,利用锐角三角函数定义及特殊角的三角函数值求出OP的长,由PQ=OQ+OP求出运动的总路程,由速度为1个单位/秒,即可求出此时的时间t;②当点P在点B左侧时,如图3所示,用∠BCO+∠BCP求出∠PCO为60°,又OC=3,在Rt△POC中,利用锐角三角函数定义及特殊角的三角函数值求出OP的长,由PQ=OQ+OP求出运动的总路程,由速度为1个单位/秒,即可求出此时的时间t;
(3)当⊙P与四边形ABCD的边(或边所在的直线)相切时,分三种情况考虑:
①当⊙P与BC边相切时,利用切线的性质得到BC垂直于CP,可得出∠BCP=90°,由∠BCO=45°,得到∠OCP=45°,即此时△COP为等腰直角三角形,可得出OP=OC,由OC=3,得到OP=3,用OQ-OP求出P运动的路程,即可得出此时的时间t;
②当⊙P与CD相切于点C时,P与O重合,可得出P运动的路程为OQ的长,求出此时的时间t;
③当⊙P与AD相切时,利用切线的性质得到∠DAO=90°,得到此时A为切点,由PC=PA,且PA=9-t,PO=t-4,在Rt△OCP中,利用勾股定理列出关于t的方程,求出方程的解得到此时的时间t.
综上,得到所有满足题意的时间t的值.
试题解析::(1)∵∠BCO=∠CBO=45°,
∴OC=OB=3,
又∵点C在y轴的正半轴上,
∴点C的坐标为(0,3);
(2)分两种情况考虑:
①当点P在点B右侧时,如图2,
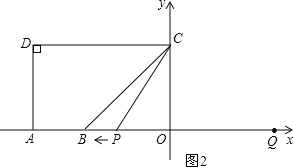
若∠BCP=15°,得∠PCO=30°,
故PO=COtan30°=![]() ,此时t=4+
,此时t=4+![]() ;
;
②当点P在点B左侧时,如图3,
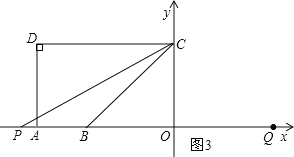
由∠BCP=15°,得∠PCO=60°,
故OP=COtan60°=3![]() ,
,
此时,t=4+3![]() ,
,
∴t的值为4+![]() 或4+3
或4+3![]() ;
;
(3)由题意知,若⊙P与四边形ABCD的边相切时,有以下三种情况:
①当⊙P与BC相切于点C时,有∠BCP=90°,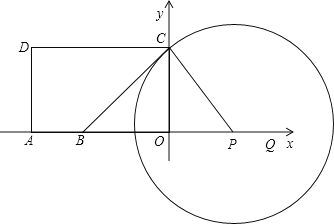
从而∠OCP=45°,得到OP=3,此时t=1;
②当⊙P与CD相切于点C时,有PC⊥CD,即点P与点O重合,此时t=4;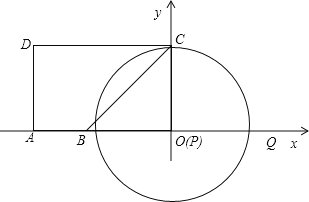
③当⊙P与AD相切时,由题意,得∠DAO=90°,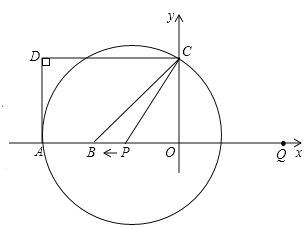
∴点A为切点,如图4,PC2=PA2=(9-t)2,PO2=(t-4)2,
于是(9-t)2=(t-4)2+32,即81-18t+t2=t2-8t+16+9,
解得:t=5.6,
∴t的值为1或4或5.6.

【题目】高速路上因赶时间超速而频频发生交通事故,这样给自己和他人的生命安全带来直接影响,为了解车速情况,一名执法交警在高速路上随机测试了6个小轿车的车速情况记录如下:
车序号 | 1 | 2 | 3 | 4 | 5 | 6 |
车速(千米/时) | 100 | 95 | 106 | 100 | 120 | 100 |
则这6辆车车速的众数和中位数(单位:千米/时)分别是( )
A.100,95
B.100,100
C.102,100
D.100,103