题目内容
【题目】如图,在四边形ABCD中,BC=CD,∠C=2∠BAD.O是四边形ABCD内一点,且OA=OB=OD.求证:
(1)∠BOD=∠C;
(2)四边形OBCD是菱形.

【答案】证明见解析
【解析】
(1)延长AO到E,利用等边对等角和角之间关系解答即可;
(2)连接OC,根据全等三角形的判定和性质以及菱形的判定解答即可.
(1)延长OA到E,如图所示:
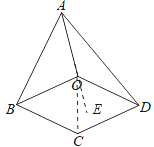
∵OA=OB,
∴∠ABO=∠BAO,
又∠BOE=∠ABO+∠BAO,
∴∠BOE=2∠BAO,
同理∠DOE=2∠DAO,
∴∠BOE+∠DOE=2∠BAO+2∠DAO=2(∠BAO+∠DAO)
即∠BOD=2∠BAD,
又∠C=2∠BAD,
∴∠BOD=∠C;
(2)连接OC,
∵OB=OD,CB=CD,OC=OC,
∴△OBC≌△ODC,
∴∠BOC=∠DOC,∠BCO=∠DCO,
∵∠BOD=∠BOC+∠DOC,∠BCD=∠BCO+∠DCO,
∴∠BOC=![]() ∠BOD,∠BCO=
∠BOD,∠BCO=![]() ∠BCD,
∠BCD,
又∠BOD=∠BCD,
∴∠BOC=∠BCO,
∴BO=BC,
又OB=OD,BC=CD,
∴OB=BC=CD=DO,
∴四边形OBCD是菱形.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
【题目】将长为![]() 、宽为
、宽为![]() 的长方形白纸,按如图所示的方法黏合起来,黏合部分宽为
的长方形白纸,按如图所示的方法黏合起来,黏合部分宽为![]() .
.

(1)根据上图,将表格补充完整:
白纸张数 | 1 | 2 | 3 | 4 | … | 10 | … |
纸条长度 | 40 | 75 | 110 | … | … |
(2)设![]() 张白纸黏合后的总长度为
张白纸黏合后的总长度为![]() ,则
,则![]() 与
与![]() 之间的关系式是 ;
之间的关系式是 ;
(3)你认为白纸黏合起来总长度可能为![]() 吗?为什么?
吗?为什么?