题目内容
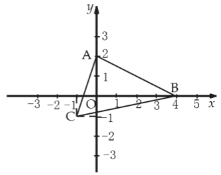
【题目】如图,在正方形ABCD中,点A在y轴正半轴上,点B的坐标为(0,﹣3),反比例函数y=﹣![]() 的图象经过点C.
的图象经过点C.
(1)求点C的坐标;
(2)若点P是反比例函数图象上的一点且S△PAD=S正方形ABCD;求点P的坐标.
【答案】(1)(5,﹣3);(2)点P的坐标为(﹣![]() ,12)或(
,12)或(![]() ,﹣8).
,﹣8).
【解析】
试题分析:(1)先由点B的坐标为(0,﹣3)得到C的纵坐标为﹣3,然后代入反比例函数的解析式求得横坐标为5,即可求得点C的坐标为(5,﹣3);
(2)设点P到AD的距离为h,利用△PAD的面积恰好等于正方形ABCD的面积得到h=10,再分类讨论:当点P在第二象限时,则P点的纵坐标yP=h+2=12,可求的P点的横坐标,得到点P的坐标为(﹣![]() ,12);②当点P在第四象限时,P点的纵坐标为yP=﹣(h﹣2)=﹣8,再计算出P点的横坐标.于是得到点P的坐标为(
,12);②当点P在第四象限时,P点的纵坐标为yP=﹣(h﹣2)=﹣8,再计算出P点的横坐标.于是得到点P的坐标为(![]() ,﹣8).
,﹣8).
解:(1)∵点B的坐标为(0,﹣3),
∴点C的纵坐标为﹣3,
把y=﹣3代入y=﹣![]() 得,﹣3=﹣
得,﹣3=﹣![]()
解得x=5,
∴点C的坐标为(5,﹣3);
(2)∵C(5,﹣3),
∴BC=5,
∵四边形ABCD是正方形,
∴AD=5,
设点P到AD的距离为h.
∵S△PAD=S正方形ABCD,
∴![]() ×5×h=52,
×5×h=52,
解得h=10,
①当点P在第二象限时,yP=h+2=12,
此时,xP=![]() =﹣
=﹣![]() ,
,
∴点P的坐标为(﹣![]() ,12),
,12),
②当点P在第四象限时,yP=﹣(h﹣2)=﹣8,
此时,xP=![]() =
=![]() ,
,
∴点P的坐标为(![]() ,﹣8).
,﹣8).
综上所述,点P的坐标为(﹣![]() ,12)或(
,12)或(![]() ,﹣8).
,﹣8).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目