题目内容
【题目】如图:梯形ABCD中,AD∥BC,∠ABC=90°,AD=4, AB=3,![]() ,在线段BC上取一点P(不与B、C重合),联结DP,作射线PQ⊥DP,PQ与直线AB交于点Q.
,在线段BC上取一点P(不与B、C重合),联结DP,作射线PQ⊥DP,PQ与直线AB交于点Q.
(1)求出梯形ABCD的面积;
(2)若点Q在边AB上,设CP=x,AQ=y,试写出y关于自变量x的函数关系式,并写出定义域.
(3)△DPC是等腰三角形,求AQ的长.
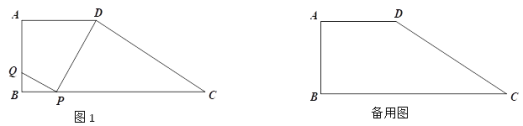
【答案】(1)21;(2)![]() ,(6≤x<10);(3)
,(6≤x<10);(3)![]() 或
或![]() .
.
【解析】
(1)作DH⊥BC,在Rt△DHC中,根据![]() ,可求出HC=6,然后按照梯形的面积公式求解即可;
,可求出HC=6,然后按照梯形的面积公式求解即可;
(2)先证明△QBP∽△PHD,根据相似三角形的性质可得![]() ,由 PC=x,所以PH=x-6,BBP=10-x,代入整理即可;
,由 PC=x,所以PH=x-6,BBP=10-x,代入整理即可;
(3)分△DPC是锐角三角形和钝角三角形两种情况求解即可.
解:(1)作DH⊥BC,
∵DH⊥BC,
∴∠DHP= ∠DHC =90°.
由题意得:AB=DH=3,AD=BH=4 ,
∵Rt△DHC中,![]() ,
,
∴![]() ,∴HC=6,
,∴HC=6,
∴BC=10 ,
∴梯形ABCD的面积![]() ;
;
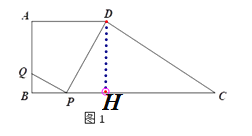
(2)∵PQ⊥DP,∠ABC=90°,
∴∠BQP=90°﹣∠QPB=∠DPH,
∵∠ABC=∠DHP=90°,
∴△QBP∽△PHD,
∴![]() ,
,
∵PC=x,∴PH=x-6,BP=10-x,
∵AQ=y,∴BQ= 3-y,
∴![]() ,
,
∴![]() ,(6≤x<10) ,
,(6≤x<10) ,
(3)当点Q在边AB上, 6≤x<10,△DPC是锐角三角形,
DP=DC,舍去,
DP=PC,舍去,
DC=PC,则![]() ,
,
![]() ,
,
当点Q在射线AB上, 0<x<6,△DPC是钝角三角形,
只有:DP=PC,设DP=PC=x,
∵Rt△DHP中,![]()
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
综上:![]() 或
或![]() .
.

【题目】某市将实行居民生活用电阶梯电价方案,如下表,图中折线反映了每户居民每月电费![]() (元)与用电量
(元)与用电量![]() (度)间的函数关系.
(度)间的函数关系.
档次 | 第一档 | 第二档 | 第三档 |
每月用电量 |
|
|
|
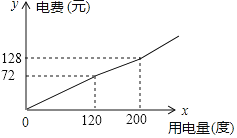
(1)小王家某月用电![]() 度,需交电费___________元;
度,需交电费___________元;
(2)求第二档电费![]() (元)与用电量
(元)与用电量![]() (度)之间的函数关系式;
(度)之间的函数关系式;
(3)小王家某月用电![]() 度,交纳电费
度,交纳电费![]() 元,请你求出第三档每度电费比第二档每度电费多多少元?
元,请你求出第三档每度电费比第二档每度电费多多少元?