题目内容
【题目】阅读理解:
材料![]() .若一元二次方程
.若一元二次方程 ![]() 的两根为
的两根为 ![]() ,
,![]() ,则
,则![]() ,
,![]() .
.
材料![]() .已知实数
.已知实数 ![]() ,
,![]() 满足
满足 ![]() ,
,![]() ,且
,且 ![]() ,求
,求![]() 的值.
的值.
解:由题知 ![]() ,
,![]() 是方程
是方程 ![]() 的两个不相等的实数根,
的两个不相等的实数根,
根据材料 ![]() 得
得 ![]() ,
,![]() ,
,
∴![]() .
.
解决问题:
(1)一元二次方程 ![]() 的两根为
的两根为 ![]() ,
,![]() ,则
,则 ![]() ,
,![]() .
.
(2)已知实数 ![]() ,
,![]() 满足
满足 ![]() ,
,![]() ,且
,且![]() ,求
,求
![]() 的值.
的值.
(3)已知实数 ![]() ,
,![]() 满足
满足 ![]() ,
,![]() ,且
,且 ![]() ,求
,求 ![]() 的值.
的值.
【答案】(1)![]() ;
;![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)直接根据根与系数的关系求解;
(2)利用m、n满足的等式,可把m、n可看作方程2x2-2x-1=0的两实数解,则根据根与系数的关系得到m+n=1,mn=-![]() ,接着把m2n+mn2分解得到mn(m+n),然后利用整体代入的方法计算;
,接着把m2n+mn2分解得到mn(m+n),然后利用整体代入的方法计算;
(3)先设t=2q,代入2q2=3q+1化简得到t2=3t+2,根据p与t满足的等式可把p与t(即2q)为方程x2-3x-2=0的两实数解,则根据根与系数的关系得到p+2q=3,p2q=-2,接着利用完全平方公式变形得到p2+4q2=(p+2q)2-2p2q,然后利用整体代入的方法计算.
解(1)x1+x2=4,x1x2=-3,
故答案为:![]() ,
,![]() ;
;
(2)∵m、n满足2m2-2m-1=0,2n2-2n-1=0,
∴m、n可看作方程2x2-2x-1=0的两实数解,
∴m+n=1,mn=-![]() ,
,
∴m2n+mn2=mn(m+n)=-![]() ×1=-
×1=-![]() ;
;
(3)设t=2q,代入2q2=3q+1化简为t2=3t+2,
则p与t(即2q)为方程x2-3x-2=0的两实数解,
∴p+2q=3,p2q=-2,
∴p2+4q2=(p+2q)2-2p2q=32-2×(-2)=13.

 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
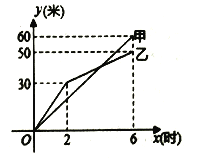
直通贵州名校周测月考直通名校系列答案【题目】某市将实行居民生活用电阶梯电价方案,如下表,图中折线反映了每户居民每月电费![]() (元)与用电量
(元)与用电量![]() (度)间的函数关系.
(度)间的函数关系.
档次 | 第一档 | 第二档 | 第三档 |
每月用电量 |
|
|
|
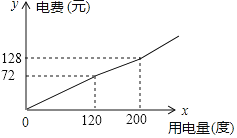
(1)小王家某月用电![]() 度,需交电费___________元;
度,需交电费___________元;
(2)求第二档电费![]() (元)与用电量
(元)与用电量![]() (度)之间的函数关系式;
(度)之间的函数关系式;
(3)小王家某月用电![]() 度,交纳电费
度,交纳电费![]() 元,请你求出第三档每度电费比第二档每度电费多多少元?
元,请你求出第三档每度电费比第二档每度电费多多少元?