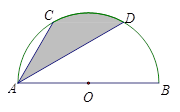
题目内容
如图,在平面直角坐标系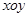 中,点
中,点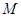 在
在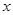 轴的正半轴上, ⊙
轴的正半轴上, ⊙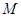 交
交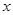 轴于
轴于 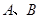 两点,交
两点,交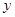 轴于
轴于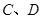 两点,且
两点,且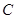 为
为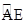 的中点,
的中点,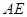 交
交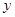 轴于
轴于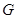 点,若点
点,若点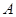 的坐标为(-2,0),
的坐标为(-2,0),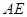
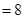
(1)求点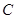 的坐标.
的坐标.
(2)连结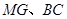 ,求证:
,求证: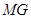 ∥
∥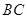
(3) 如图10-2,过点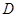 作⊙
作⊙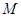 的切线,交
的切线,交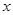 轴于点
轴于点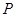 .动点
.动点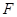 在⊙
在⊙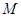 的圆周上运动时,
的圆周上运动时,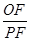 的比值是否发生变化,若不变,求出比值;若变化,说明变化规律
的比值是否发生变化,若不变,求出比值;若变化,说明变化规律
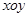 中,点
中,点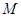 在
在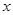 轴的正半轴上, ⊙
轴的正半轴上, ⊙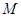 交
交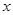 轴于
轴于 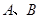 两点,交
两点,交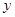 轴于
轴于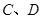 两点,且
两点,且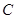 为
为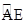 的中点,
的中点,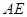 交
交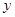 轴于
轴于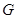 点,若点
点,若点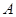 的坐标为(-2,0),
的坐标为(-2,0),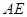
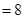

(1)求点
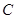 的坐标.
的坐标. (2)连结
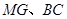 ,求证:
,求证: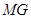 ∥
∥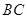
(3) 如图10-2,过点
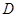 作⊙
作⊙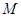 的切线,交
的切线,交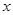 轴于点
轴于点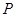 .动点
.动点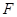 在⊙
在⊙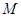 的圆周上运动时,
的圆周上运动时,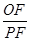 的比值是否发生变化,若不变,求出比值;若变化,说明变化规律
的比值是否发生变化,若不变,求出比值;若变化,说明变化规律1)(0,4) (2)通过证明MF是中位线来证明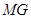 ∥
∥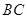 (3)
(3)
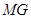 ∥
∥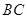 (3)
(3)
试题分析:(1)⊙
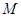 交
交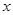 轴于
轴于 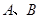 两点,交
两点,交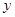 轴于
轴于 两点,且
两点,且 为
为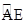 的中点,弧AE等于弧CD,所以CD=AE;OC=
的中点,弧AE等于弧CD,所以CD=AE;OC=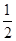 AE=4,因此点
AE=4,因此点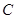 的坐标(0,4)
的坐标(0,4)(2)连结
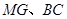 、AC,延长MG交 AC于F,由题意可得F是AC的中点,M是AB的中点,所以MF是
、AC,延长MG交 AC于F,由题意可得F是AC的中点,M是AB的中点,所以MF是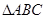 的中位线,所以
的中位线,所以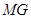 ∥
∥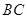
(3)
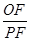 的比值不会发生变化,
的比值不会发生变化,过点
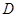 作⊙
作⊙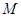 的切线,交
的切线,交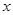 轴于点
轴于点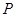 .动点
.动点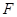 在⊙
在⊙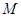 的圆周上运动时,根据题意
的圆周上运动时,根据题意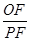 =
=
点评:本题考查圆的知识,掌握圆的概念和性质是解本题的关键,圆是中考比考内容

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
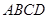 内, 半径为2的⊙
内, 半径为2的⊙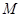 与边
与边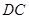 和
和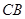
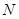 与⊙
与⊙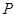 , 并且
, 并且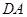 和
和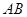 相切.
相切. 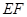 是两圆的内公切线, 点
是两圆的内公切线, 点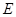 和
和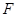 分别在
分别在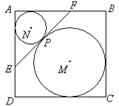
 为
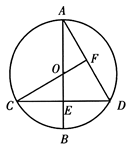
为 上一点,点
上一点,点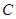 在直径
在直径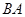 的延长线上,
的延长线上,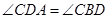 .
.
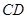 是
是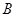 作
作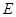 ,若BC=4,tan∠ABD=
,若BC=4,tan∠ABD=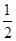 求
求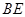 的长.
的长.
 .
.