题目内容
如图, 边长是5的正方形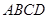 内, 半径为2的⊙
内, 半径为2的⊙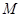 与边
与边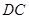 和
和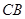
相切, ⊙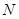 与⊙
与⊙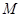 外切于点
外切于点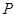 , 并且
, 并且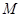 与边
与边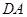 和
和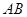 相切.
相切. 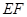 是两圆的内公切线, 点
是两圆的内公切线, 点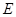 和
和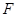 分别在
分别在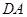 和
和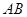 上. 则
上. 则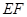 的长等于 _______ .
的长等于 _______ .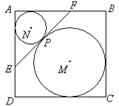
 内, 半径为2的⊙
内, 半径为2的⊙ 与边
与边 和
和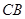
相切, ⊙
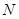 与⊙
与⊙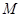 外切于点
外切于点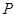 , 并且
, 并且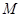 与边
与边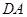 和
和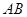 相切.
相切. 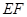 是两圆的内公切线, 点
是两圆的内公切线, 点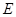 和
和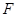 分别在
分别在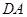 和
和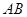 上. 则
上. 则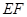 的长等于 _______ .
的长等于 _______ .
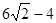
试题分析:由题意分析可知,设AB交圆N于点P,交AD于点Q
所以FP=EQ
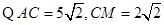
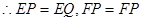

点评:圆与圆的位置关系判断条件,确定位置关系.设两圆的半径分别为R和r,且R≥r,圆心距为d:外离,则d>R+r;外切,则d=R+r;相交,则R-r<d<R+r;内切,则d=R-r;内含,则d<R-r.

练习册系列答案
相关题目
 cm的⊙O从斜坡上的A点处沿斜坡滚动到平地上的C点处,已知∠ABC=120°,AB="10" cm,BC=20cm,那么圆心O运动所经过的路径长度为
cm的⊙O从斜坡上的A点处沿斜坡滚动到平地上的C点处,已知∠ABC=120°,AB="10" cm,BC=20cm,那么圆心O运动所经过的路径长度为
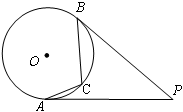
 是
是 的外接圆,
的外接圆, 是
是 ,
, ,则
,则 的值是( )
的值是( )


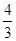
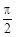 ,则BC= .
,则BC= .
 ,则这条弦的中点到弦所对优弧的中点的距离为( )
,则这条弦的中点到弦所对优弧的中点的距离为( ) )cm
)cm
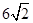
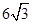
 中,点
中,点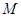 在
在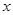 轴的正半轴上, ⊙
轴的正半轴上, ⊙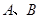 两点,交
两点,交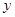 轴于
轴于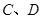 两点,且
两点,且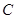 为
为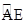 的中点,
的中点,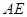 交
交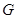 点,若点
点,若点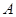 的坐标为(-2,0),
的坐标为(-2,0),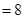
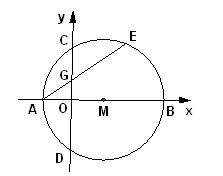
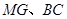 ,求证:
,求证: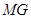 ∥
∥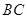
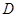 作⊙
作⊙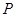 .动点
.动点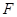 在⊙
在⊙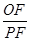 的比值是否发生变化,若不变,求出比值;若变化,说明变化规律
的比值是否发生变化,若不变,求出比值;若变化,说明变化规律