题目内容
【题目】如图，将矩形纸片ABCD中，AB＝6，BC＝9，沿EF折叠，使点B落在DC边上点P处，点A落在Q处，AD与PQ相交于点H．
（1）如图1，当点P为边DC的中点时，求EC的长；
（2）如图2，当∠CPE＝30°，求EC、AF的长；（3）如图2，在（2）条件下，求四边形EPHF的面积．
【答案】（1）4；（2）6﹣2
；（3）72﹣30
【解析】
（1）由题意可知PC=3,由翻折的性质可知BE=PE，设EC=x，则PE=9-x，在Rt△PEC中根据勾股定理列方程解答即可；
（2）依据含30°角的直角三角形的性质可知EC与PE关系，设EC=x，则EB=9-x，由翻折的性质可知EP=BE=9-x，列出关于x的方程可求出EC的长，然后利用特殊锐角三角函数值，可求出PC、PD、DH的长，然后设AF=y，由翻折的性质可知AF=QF=y，最后依据FQ=
FH列方程解答即可；
（3）连接EH，先求出FH和PH、PE的长，最后依据四边形FEPH的面积等于△FHE的面积加△HPE面积求解即可。
解：（1）∵ABCD为矩形，∴CD＝AB＝6．∵P是DC的中点，∴PC＝3．
由翻折的性质可知BE＝PE．设EC＝x，则PE＝9﹣x．
在Rt△PEC中，依据勾股定理可知：PE2＝EC2+PC2，即（9﹣x）2＝x2+32，解得：x＝4，
∴EC＝4．
（2）∵∠CPE＝30°，∠C＝90°，∴EC＝
PE．
设EC＝x，则EB＝9﹣x，由翻折的性质可知EP＝BE＝9﹣x．
∵EC＝PE，∴x＝×（9﹣x）．解得：x＝3．∴EC＝3．
∴
＝
，则CP＝3
．∴DP＝6﹣3．∵∠EPH＝90°，∠CPE＝30°，
∴∠DPH＝60°．∴DH＝DP＝6﹣9．∴AH＝18﹣6．
设AF＝y，由翻折的性质可知AF＝QF＝y，则FH＝18﹣6﹣y．
∵∠QHF＝30°，∠Q＝90°，∴QF＝
FH．
∴y＝×（18﹣6﹣y），解得：y＝6﹣2．
∴AF＝6﹣2
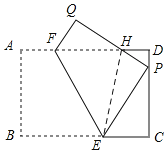
（3）如图所示：连结EH．
由（2）可知AF＝6﹣2
，∴FH＝18﹣6﹣（6﹣2）＝12﹣4．
∵PH＝2DP，EP＝2EC，∴PH＝12﹣6，PE＝6．
∴四边形FEPH的面积＝△FHE的面积+△HPE的面积＝
FHAB+HPEP
＝
（12﹣4
）×6+
×（12﹣6）×6＝72﹣30．
