题目内容
【题目】如图,直角△ABC中,∠BAC=90°,D在BC上,连接AD,作BF⊥AD分别交AD于E,AC于F.
(1)如图1,若BD=BA,求证:△ABE≌△DBE;
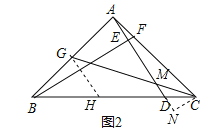
(2)如图2,若BD=4DC,取AB的中点G,连接CG交AD于M,求证:①GM=2MC;②AG2=AFAC.

【答案】(1)证明见解析;(2)①证明见解析;②证明见解析.
【解析】
试题分析:(1)根据全等三角形的判定定理即可得到结论;
(2)①过G作GH∥AD交BC于H,由AG=BG,得到BH=DH,根据已知条件设DC=1,BD=4,得到BH=DH=2,根据平行线分线段成比例定理得到![]() ,求得GM=2MC;
,求得GM=2MC;
②过C作CN⊥AD交AD的延长线于N,则CN∥AG,根据相似三角形的性质得到![]() ,由①知GM=2MC,得到2NC=AG,根据相似三角形的性质得到
,由①知GM=2MC,得到2NC=AG,根据相似三角形的性质得到![]() ,等量代换得到
,等量代换得到![]() ,于是得到结论.
,于是得到结论.
试题解析:(1)在Rt△ABE和Rt△DBE中,∵BA=BD,BE=BE,∴△ABE≌△DBE;
(2)①过G作GH∥AD交BC于H,∵AG=BG,∴BH=DH,∵BD=4DC,设DC=1,BD=4,∴BH=DH=2,∵GH∥AD,∴![]() ,∴GM=2MC;
,∴GM=2MC;
②过C作CN⊥AC交AD的延长线于N,则CN∥AG,∴△AGM∽△NCM,∴![]() ,由①知GM=2MC,∴2NC=AG,∵∠BAC=∠AEB=90°,∴∠ABF=∠CAN=90°﹣∠BAE,∴△ACN∽△BAF,∴
,由①知GM=2MC,∴2NC=AG,∵∠BAC=∠AEB=90°,∴∠ABF=∠CAN=90°﹣∠BAE,∴△ACN∽△BAF,∴![]() ,∵AB=AG,∴
,∵AB=AG,∴![]() ,∴2CNAG=AFAC,∴AG2=AFAC.
,∴2CNAG=AFAC,∴AG2=AFAC.

【题目】在水果销售旺季,某水果店购进一优质水果,进价为 20 元/千克,售价不低于 20 元/千克,且不超过 32 元/千克,根据销售情况,发现该水果一天的销售量 y(千克)与该天的售价 x(元/千克)满足如下表所示的一次函数关系.
销售量 y(千克) | … | 34.8 | 32 | 29.6 | 28 | … |
售价 x(元/千克) | … | 22.6 | 24 | 25.2 | 26 | … |
(1)某天这种水果的售价为 23.5 元/千克,求当天该水果的销售量.
(2)如果某天销售这种水果获利 150 元,那么该天水果的售价为多少元?





