Question

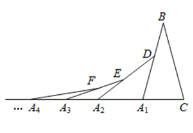
【题目】如图，BD是等边三角形ABC的角平分线，E是BC延长线上的一点，且CE=CD，DF=BC，垂足为F．BF与EF相等吗？为什么？

Answer 1

【答案】BF与EF相等，证明见解析.

【解析】

根据等边三角形的性质得∠ABC=∠ACB=60°，再由BD是角平分线得∠CBD=30°，接着根据等腰三角形的性质，由CD=CE得到∠CDE=∠E，利用三角形外角性质可计算出∠E=30°，所以∠DBE=∠E，于是可判断△DBE为等腰三角形，然后根据等腰三角形的性质可得BF=EF．

BF与EF相等。理由如下：

∵△ABC为等边三角形，

∴∠ABC=∠ACB=60°，

∵BD是等边三角形ABC的角平分线，

∴∠CBD=30°，

∵CD=CE，

∴∠CDE=∠E，

而∠BCD=∠CDE+∠E=60°，

∴∠E=30°，

∴∠DBE=∠E，

∴△DBE为等腰三角形，

∵DF⊥BC，

∴BF=EF.