题目内容
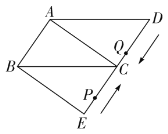
【题目】已知,![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 边中点,连接
边中点,连接![]() ,点
,点![]() 为
为![]() 的中点,线段
的中点,线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() ,
,![]() .
.
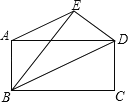
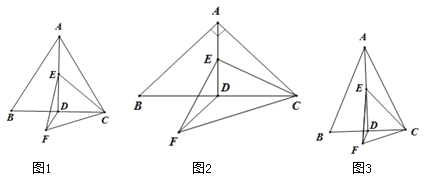
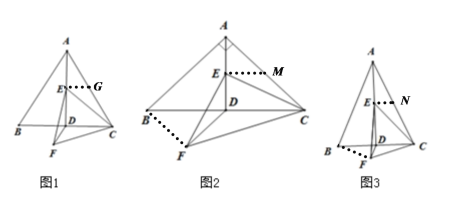
(1)如图1,当![]() 时,请直接写出
时,请直接写出![]() 的值;
的值;
(2)如图2,当![]() 时,(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请写出正确的结论,并说明理由;
时,(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请写出正确的结论,并说明理由;
(3)如图3,当![]() 时,请直接写出
时,请直接写出![]() 的值(用含
的值(用含![]() 的三角函数表示).
的三角函数表示).
【答案】(1)![]() ;(2)不成立,
;(2)不成立,![]() ,理由见解析;(3)
,理由见解析;(3)![]() .
.
【解析】
(1)如图1(见解析),先根据中位线定理得出![]() ,再根据旋转的性质、等边三角形的性质得出
,再根据旋转的性质、等边三角形的性质得出![]() ,
,![]() ,
,![]() ,然后根据三角形全等的判定定理与性质可得
,然后根据三角形全等的判定定理与性质可得![]() ,由此即可得出答案;
,由此即可得出答案;
(2)如图2(见解析),先根据中位线定理、等腰三角形的三线合一得出![]() ,再根据等腰直角三角形的性质得出
,再根据等腰直角三角形的性质得出![]() ,
,![]() ,然后根据相似三角形的判定与性质可得
,然后根据相似三角形的判定与性质可得![]() ,
,![]() ,从而可得
,从而可得![]() ,最后根据相似三角形的判定与性质可得
,最后根据相似三角形的判定与性质可得![]() ,据此利用正弦三角函数值即可得;
,据此利用正弦三角函数值即可得;
(3)如图3(见解析),参照题(2)的思路,先根据相似三角形的判定与性质得出![]() ,再在
,再在![]() 中,利用正弦三角函数值即可得.
中,利用正弦三角函数值即可得.
(1)如图1,取AC的中点G,连接EG,则![]()
![]() 点
点![]() 为
为![]() 的中点
的中点
![]() 是
是![]() 的中位线
的中位线
![]() ,即
,即![]()
由旋转的性质可知,![]() ,
,![]()
![]() 是等边三角形
是等边三角形
![]() ,
,![]()
![]() ,
,![]()
![]() 是等边三角形
是等边三角形
![]()
![]() 点
点![]() 为
为![]() 边中点
边中点
![]()
![]() ,
,![]()
![]()
在![]() 和
和![]() 中,
中,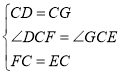
![]()
![]()
![]() ;
;
(2)不成立,![]() ,理由如下:
,理由如下:
如图2,连接![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]()
∵![]() 是
是![]() 的中点
的中点
∴![]()
∴![]()
∵![]()
![]() 是等腰三角形
是等腰三角形
∵![]() 是
是![]() 中点,
中点, ![]()
∴![]() ,
,![]() ,
,![]()
∴![]()
∴![]()
当![]() 时,则
时,则![]()
![]() 和
和![]() 为等腰直角三角形
为等腰直角三角形
∴![]() ,即
,即![]()
∴![]() ,
,![]()
∴![]()
∴![]() ,
,![]()
∵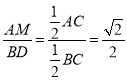
∴![]()
∴![]()
∴![]()
在![]() 中,
中,![]() ,即
,即![]()
则![]() ;
;
(3)![]() ,求解过程如下:
,求解过程如下:
如图3,连接![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]()
参照(2),同理可得:![]() ,
,![]() ,
,![]()
当![]() 时,则
时,则![]()
![]() ,
,![]() (旋转的性质)
(旋转的性质)
![]() 和
和![]() 为等腰三角形
为等腰三角形
∴![]()
![]()
![]()
![]()
![]()
又![]()
∴![]()
∴![]()
∴![]() ,
,![]()
∵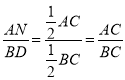
∴![]()
∴![]()
∴![]()
在![]() 中,
中,![]()
即![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】某小学三年级到六年级的全体学生参加“礼仪”知识测试,现将有关数据整理后绘制成如下“年级人数统计图”和尚未全部完成的“成绩情况统计表”![]() 根据图表中提供的信息,回答下列问题:
根据图表中提供的信息,回答下列问题:

成绩 | 100分 | 90分 | 80分 | 70分 | 60分 |
人数 | 21 | 40 | 5 | ||
频率 |
|
(1)测试学生中,成绩为80分的学生人数有___名;众数是___分;中位数是___分;
![]() 若该小学三年级到六年级共有1800名学生,则可估计出成绩为70分的学生人数约有多少名?
若该小学三年级到六年级共有1800名学生,则可估计出成绩为70分的学生人数约有多少名?