题目内容
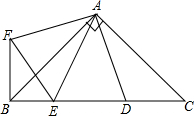
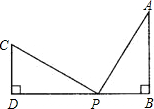
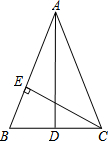
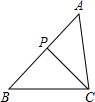
如图,P是△ABC中边AB上一点,连接CP,有如下条件:①∠ACP=∠B,②∠APC=∠ACB,③AC2=AP•AB,④
=
,其中能判定△ACP∽△ABC的条件是______(填序号).
| AC |
| CP |
| AB |
| BC |

由图可知,∠A为△ACP和△ABC的公共角,
①∠ACP=∠B,符合两角对应相等,两三角形相似,
②∠APC=∠ACB,符合两角对应相等,两三角形相似,
③由AC2=AP•AB可得
=
,符合两边对应成比例,夹角相等,两三角形相似,
④
=
,夹角为∠B,可判定△CBP∽△ABC,
所以能判定△ACP∽△ABC的条件是①②③.
故答案为:①②③.
①∠ACP=∠B,符合两角对应相等,两三角形相似,
②∠APC=∠ACB,符合两角对应相等,两三角形相似,
③由AC2=AP•AB可得
| AC |
| AP |
| AB |
| AC |
④
| AC |
| CP |
| AB |
| BC |
所以能判定△ACP∽△ABC的条件是①②③.
故答案为:①②③.

练习册系列答案
相关题目