题目内容
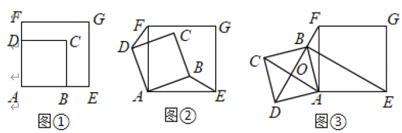
【题目】如图①,四边形![]() 是边长为2的正方形,
是边长为2的正方形,![]() ,四边形
,四边形![]() 是边长为
是边长为![]() 的正方形,点
的正方形,点![]() 分别在边
分别在边![]() 上,此时
上,此时![]() ,
,![]() 成立.
成立.
(1)当正方形![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,如图②,
,如图②,![]() 成立吗?若成立,请证明;若不成立,请说明理由;
成立吗?若成立,请证明;若不成立,请说明理由;
(2)当正方形![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() (任意角)时,
(任意角)时,![]() 仍成立吗?直接回答;
仍成立吗?直接回答;
(3)连接![]() ,当正方形
,当正方形![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 时,是否存在
时,是否存在![]() ∥
∥![]() ,若存在,请求出
,若存在,请求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)成立,证明见解析;(2)结论仍成立;(3)存在,![]()
【解析】
(1)先利用正方形的性质和旋转的性质证明![]() ≌
≌![]() ,然后得出
,然后得出![]() ,再根据等量代换即可得出
,再根据等量代换即可得出![]() ,则有
,则有![]() ;
;
(2)先利用正方形的性质和旋转的性质证明![]() ≌
≌![]() ,然后得出
,然后得出![]() ,再根据等量代换即可得出
,再根据等量代换即可得出![]() ,则有
,则有![]() ;
;
(3)通过分析得出![]() 时,
时,![]() 在同一直线上,根据AO,AF求
在同一直线上,根据AO,AF求![]() ,从而有
,从而有![]() ,最后利用
,最后利用![]() 即可求解.
即可求解.
(1)结论![]() ,
,![]() 仍成立.
仍成立.
如图1,延长![]() 交
交![]() 于
于![]() 交
交![]() 于点
于点![]() ,
,

∵四边形![]() ,ABCD都是正方形,
,ABCD都是正方形,
∴![]() .
.
由旋转可得,![]() ,
,
![]() ,
,
∴![]() ≌
≌![]() ,
,
∴![]() .
.
![]()
![]() ,
,
![]() ,
,
∴![]() ,
,
∴结论仍成立 .
(2)若正方形![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 时,如图,结论仍然成立,理由如下:
时,如图,结论仍然成立,理由如下:

如图2,延长![]() 交
交![]() 于
于![]() 交
交![]() 于点
于点![]() ,
,
∵四边形![]() ,ABCD都是正方形,
,ABCD都是正方形,
∴![]() .
.
由旋转可得,![]() ,
,
![]() ,
,
∴![]() ≌
≌![]() ,
,
∴![]() .
.
![]()
![]() ,
,
![]() ,
,
∴![]() ,
,
∴结论仍成立 .
当旋转其他角度时同理可证![]() ,所以结论仍成立.
,所以结论仍成立.
(3)存在
如图3,连接![]() ,与
,与![]() 相交于
相交于![]() ,
,

∵![]() ,当
,当![]() ∥
∥![]() 时,
时,![]() ,
,
又∵![]() ,
,
∴![]() 在同一直线上.
在同一直线上.
∵四边形ABCD,AEGF是正方形,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
![]() ,
,
![]() ,
,
∴![]() ,
,
![]()
即当![]() 时,
时,![]() ∥
∥![]() 成立.
成立.

【题目】在一个不透明的袋子中装有除颜色外其余均相同的m个小球,其中 5 个黑球, 从袋中随机摸出一球,记下其颜色,这称为依次摸球试验,之后把它放回袋 中,搅匀后,再继续摸出一球.以下是利用计算机模拟的摸球试验次数与摸出黑球次数的列表:
摸球试验次数 | 100 | 1000 | 5000 | 10000 | 50000 | 100000 |
摸出黑球次数 | 46 | 487 | 2506 | 5008 | 24996 | 50007 |
根据列表,可以估计出 m 的值是( )
A. 5 B. 10 C. 15 D. 20