题目内容
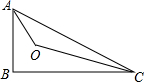
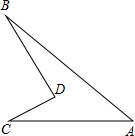
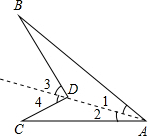
如图,∠BDC=98°,∠C=38°,∠B=23°,∠A的度数是( )
| A.61° | B.60° | C.37° | D.39° |

作直线AD,
∴∠3=∠B+∠1---(1)
∴∠4=∠C+∠2---(2)
由(1)、(2)得:∠3+∠4=∠B+∠C+∠1+∠2,
即∠BDC=∠B+∠C+∠BAC,
∵∠BDC=98°,∠C=38°,∠B=23°
∴∠BAC=98°-38°-23°=37°.
故选C.
∴∠3=∠B+∠1---(1)
∴∠4=∠C+∠2---(2)
由(1)、(2)得:∠3+∠4=∠B+∠C+∠1+∠2,
即∠BDC=∠B+∠C+∠BAC,
∵∠BDC=98°,∠C=38°,∠B=23°
∴∠BAC=98°-38°-23°=37°.
故选C.


练习册系列答案
相关题目