题目内容
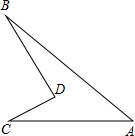
如图，D是△ABC的边BC上的一点，且AB=CD，∠BAD=34.5°，∠B=37°，则∠C=______度．
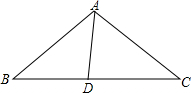
由AB=CD，如图将△ABD移动到△CDE，
∴AD=CE，BD=DE，∠B=∠CDE=37°，∠BAD=∠DCE=34.5°，
根据三角形外角性质，
∠ADC=∠B+∠BAD=71.5°，
∴∠ADE=∠ADC+∠CDE=108.5°，
根据三角形内角和等于180°，
∠E=∠ADB=180°-∠B-∠BAD=108.5°，
即：∠ADE=∠E，
又AD=CE，
∴梯形ADEC为等腰梯形，
∴∠ACD=∠CDE=37°．
∴AD=CE，BD=DE，∠B=∠CDE=37°，∠BAD=∠DCE=34.5°，
根据三角形外角性质，
∠ADC=∠B+∠BAD=71.5°，
∴∠ADE=∠ADC+∠CDE=108.5°，
根据三角形内角和等于180°，
∠E=∠ADB=180°-∠B-∠BAD=108.5°，
即：∠ADE=∠E，
又AD=CE，
∴梯形ADEC为等腰梯形，
∴∠ACD=∠CDE=37°．
练习册系列答案
阅读快车系列答案
相关题目
