Question

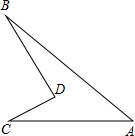
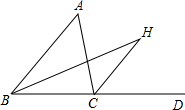
如图，在△ABC中，CH是外角∠ACD的平分线，BH是∠ABC的平分线．
（1）求证：∠A=2∠H；
（2）若△ABC中，AB=AC，当∠A等于多少度时，AB∥HC．

Answer 1

（1）证明：∵BH、CH分别是∠ABC、∠ACD的平分线，
∴∠ABC=2∠1，∠ACD=2∠2，
∵∠HCD是△BCH的外角，
∴∠H=∠HCD-∠HBC=∠2-∠1，
∵∠ACD是△ABC的外角，
∴∠A=∠ACD-∠ABC=2∠2-2∠1=2（∠2-∠1）=2∠H；

（2）设∠A=x由（1）得∠H=

x

2

，
∵AB=AC，
∴∠ABC=

180°-x

2

，
∵BH是∠ABC的平分线，
∴∠1=

180°-x

4

，
∵∠HCD是△BCH的外角，
∴∠2=∠1+∠H=

180°-x

4

+

x

2

，
要使得AB∥CH，则必须满足∠ABC=∠2
∴

180°-x

2

=

180°-x

4

+

x

2

，解得x=60°
∴当∠A等于60°时，AB∥HC．