Question

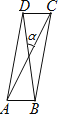
【题目】如图，在□ABCD中，对角线 AC、BD 相交成的锐角α=30°，若 AC=8，BD=6，则□ABCD的面积是( )

A.6B.8C.10D.12

Answer 1

【答案】D

【解析】

如图，过点D作DE⊥AC于E点，设AC与BD相交于O点，首先根据平行四边形性质得出DO=3，然后利用直角三角形中30°角所对的直角边等于斜边的一半求出DE，由此得出△ACD的面积，最后进一步通过证明△ADC△CBA得出△CBA的面积=△ADC的面积，从而即可得出答案.

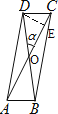
如图，过点D作DE⊥AC于E点，设AC与BD相交于O点，

∵在平行四边形ABCD中，AC=8，BD=6，

∴DO=，

∵∠α=30°，DE⊥AC，

∴DE=，

∴△ACD的面积=，

∵四边形ABCD为平行四边形，

∴CD=AB，AD=BC，

在△ADC与△CBA中，

∵AD=CB，CD=AB，AC=CA，

∴△ADC△CBA（SSS），

∴△CBA的面积=△ADC的面积=6，

∴该平行四边形的面积=△CBA的面积+△ADC的面积=12，

故选：D.