题目内容
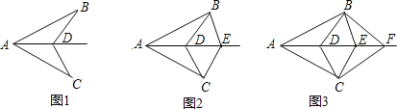
【题目】操作:在△ABC中,AC=BC=2,∠C=90°,将一块等腰三角形板的直角顶点放在斜边AB的中点P处,将三角板绕点P旋转,三角板的两直角边分别交射线AC、CB于D、E两点。图①,②,③是旋转三角板得到的图形中的3种情况。研究:
(1)三角板ABC绕点P旋转,观察线段PD和PE之间有什么数量关系?并结合图②加以证明。
(2)三角板ABC绕点P旋转,△PBE是否能为等腰三角形?若能,指出所有情况(即写出△PBE为等腰三角形时CE的长);若不能,请说明理由。(图④不用)

【答案】(1)PD=PE;(2)CE=0或1.
【解析】
试题分析:连接PC,根据题意得出CP=PB,∠ACP=∠B=45°,∠DPC=∠BPE,从而得出△PCD和△PBE全等,从得出答案;第二题分PE=PB,PB=BE和PE=BE三种情况分别进行讨论.
试题解析:(1)由图①可猜想PD=PE,再在图②中构造全等三角形来说明.即PD=PE.
理由如下:连接PC,因为△ABC是等腰直角三角形,P是AB的中点,∴CP=PB,CP⊥AB,∠ACP= ∠ACB=45°.
∴∠ACP=∠B=45°.又∠DPC+∠CPE=∠BPE+∠CPE,∴∠DPC=∠BPE.
∴△PCD≌△PBE. ∴PD=PE.
(2)△PBE是等腰三角形,
①当PE=PB时,此时点C与点E重合,CE=0;
②当PB=BE时,1)E在线段BC上, ,2)E在CB的延长线上,
③当PE=BE时,CE=1.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目