题目内容
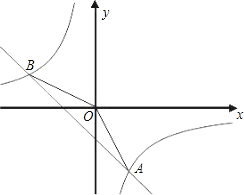
【题目】已知一次函数y= kx+b的图象与反比例函数![]() 的图象相交于A,B两点, 其中A点的横坐标与B点的纵坐标都是2,如图:
的图象相交于A,B两点, 其中A点的横坐标与B点的纵坐标都是2,如图:
(1)求这个一次函数的解析式;
(2)在y轴是否存在一点P使△OAP为等腰三角形?若存在,请求出符合条件的点P坐标;若不存在,请说明理由.
【答案】(1)y=-x-2;(2)见解析
【解析】试题分析:(1)首先根据反比例函数解析式分别求出A、B两个点的坐标,再设一次函数解析式为一般形式,将两个点的坐标代入求出未知参数即可;(2)分三种情况,①OA=OP, ②OA=AP,③ OP=AP,结合圆对每个情况依次求解即可.
试题解析:
(1)反比例函数y=![]() 的图象经过A,B两点,且A点的横坐标与B点的纵坐标都是2;
的图象经过A,B两点,且A点的横坐标与B点的纵坐标都是2;
∴当x=2时,y =-4;当y=2时,x=-4
∴A点的坐标为(2,-4),B点的坐标为(-4,2);
∵y=kx+b(k≠0)经过A,B两点;
∴把A(2,-4),B(-4,2)代入y=kx+b(k≠0)得:
![]() ,
,
解得:k=-1,b=-2;
把k=-1,b=-2代入y=k x+b(k≠0)得:y=-x-2;
(2)OA=![]() =2
=2![]() ,OB=
,OB=![]() =2
=2![]() .
.
假设存在点P,使△OAP为等腰三角形,分三种情况,
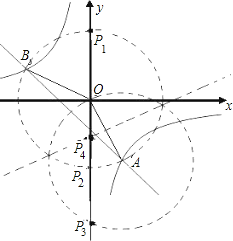

OA=OP,以O为圆心,OA的长为半径画圆弧,与y轴的交点即为符合条件的点P,则P1(0, ![]() ) , P2 (0,
) , P2 (0, ![]() ) ;
) ;
OA=AP,以A为圆心,OA为半径画圆弧,与y轴的交点即为符合条件的点P,作AD⊥y轴交y轴与点D,
∴OD=DP3=4,
∴P3(0,-8);
OP=AP,作OA的垂直平分线分别交y轴于点P4,交AO于点E,垂直平分线与y轴的交点即为符合条件的点P.
∴OE=![]() ,
,
∵cos∠EOP4=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴OP4=![]() ,
,
∴P4 (0, ![]() ).
).

练习册系列答案
相关题目