Question

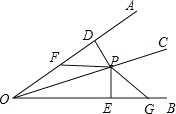
【题目】如图，已知线段AC∥y轴，点B在第一象限，且AO平分∠BAC，AB交y轴与G，连OB、OC．

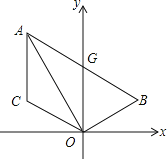
（1）判断△AOG的形状，并予以证明；

（2）若点B、C关于y轴对称，求证：AO⊥BO．

Answer 1

【答案】（1）等腰三角形；证明见解析；（2）证明见解析.

【解析】

（1）易证∠CAO＝∠AOG和∠CAO＝∠GAO，即可判定△AOG是等腰三角形；

（2）连接BC交y轴于K，过A作AN⊥y轴于N，易证△ANG≌△BKG，即可证明∠BOG＝∠OBG，∠OAG＝∠AOG，根据三角形内角和为180°即可解题．

解：（1）△AOG是等腰三角形；

证明：∵AC∥y轴，

∴∠CAO＝∠AOG，

∵AO平分∠BAC，

∴∠CAO＝∠GAO，

∴∠GAO＝∠AOG，

∴AG＝GO，

∴△AOG是等腰三角形；

（2）连接BC交y轴于K，过A作AN⊥y轴于N，

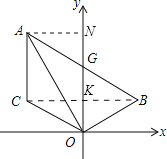
∵AC∥y轴，点B、C关于y轴对称，

∴AN＝CK＝BK，

在△ANG和△BKG中，

，

∴△ANG≌△BKG（AAS），

∴AG＝BG，

∵AG＝OG，（1）中已证，

∴AG＝OG＝BG，

∴∠BOG＝∠OBG，∠OAG＝∠AOG，

∵∠OAG+∠AOG+∠BOG+∠OBG＝180°，

∴∠AOG+∠BOG＝90°，

∴AO⊥BO．