题目内容
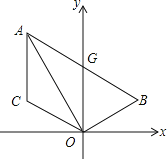
【题目】如图,点A(m,m+1),B(m+1,2m-3)都在反比例函数![]() 的图象上.
的图象上.
(1)求m,k的值;
(2)如果M为x轴上一点,N为y轴上一点, 以点A,B,M,N为顶点的四边形是平行四边形,试求直线MN的函数表达式.
【答案】(1)m=3,k=12;(2)![]() 或
或![]()
【解析】
试题分析:(1)根据反比例函数图象上的点的坐标的特征可得![]() ,即可求得结果;
,即可求得结果;
(2)存在两种情况,①当M点在x轴的正半轴上,N点在y轴的正半轴上时,②当M点在x轴的负半轴上,N点在y轴的负半轴上时,根据平行四边形的性质求解即可.
(1)由题意可知,![]()
解得m1=3,m2=-1(舍去)
∴A(3,4),B(4,3);
∴k=4×3=12;
(2)存在两种情况,如图:
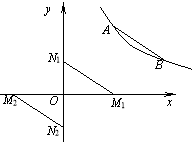
①当M点在x轴的正半轴上,N点在y轴的正半轴上时,设M1点坐标为(x1,0),N1点坐标为(0,y1).
∵四边形AN1M1B为平行四边形,
∴线段N1M1可看作由线段AB向左平移3个单位,再向下平移3个单位得到的
由(1)知A点坐标为(3,4),B点坐标为(4,3),
∴N1点坐标为(0,1),M1点坐标为(1,0)
设直线M1N1的函数表达式为![]() ,把x=1,y=0代入,解得
,把x=1,y=0代入,解得![]() .
.
∴直线M1N1的函数表达式为![]() ;
;
②当M点在x轴的负半轴上,N点在y轴的负半轴上时,设M2点坐标为(x2,0),N2点坐标为(0,y2).
∵AB∥N1M1,AB∥M2N2,AB=N1M1,AB=M2N2,
∴N1M1∥M2N2,N1M1=M2N2.
∴线段M2N2与线段N1M1关于原点O成中心对称.
∴M2点坐标为(-1,0),N2点坐标为(0,-1).
设直线M2N2的函数表达式为![]() ,把x=-1,y=0代入,解得
,把x=-1,y=0代入,解得![]() ,
,
∴直线M2N2的函数表达式为![]()
所以,直线MN的函数表达式为![]() 或
或![]() .
.

【题目】为弘扬中华传统文化,某校组织八年级800名学生参加汉字听写大赛为了解学生整体听写能力,从中抽取部分学生的成绩(得分取正整数,满分为100分)进行统计分析,得到如下所示的模数分布表:
分数段 | 50.5﹣60.5 | 60.5﹣70.5 | 70.5﹣80.5 | 80.5﹣90.5 | 90.5﹣100.5 |
频数 | 16 | 30 | 50 | m | 24 |
所占百分比 | 8% | 15% | 25% | 40% | n |
请根据尚未完成的表格,解答下列问题:
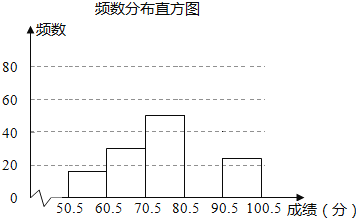
(1)本次抽样调查的样本容量为 ,表中m= .n
(2)补全图中所示的频数分布直方图;
(3)若成绩超过80分为优秀,则该校八年级学生中汉字听写能力优秀的约有多少人?