题目内容
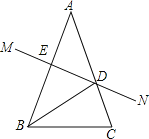
【题目】已知:如图,P是OC上一点,PD⊥OA于D,PE⊥OB于E,F、G分别是OA、OB上的点,且PF=PG,DF=EG.
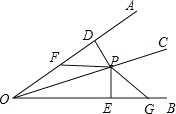
(1)求证:OC是∠AOB的平分线.
(2)若PF∥OB,且PF=4,∠AOB=30°,求PE的长.
【答案】(1)证明见解析;(2)PE=2.
【解析】
(1)利用“HL”证明Rt△PFD和Rt△PGE全等,根据全等三角形对应边相等可得PD=PE,再根据到角的两边距离相等的点在角的平分线上证明即可;
(2)在Rt△PFD中,求出PD即可解决问题.
(1)证明:在Rt△PFD和Rt△PGE中,
![]() ,
,
∴Rt△PFD≌Rt△PGE(HL),
∴PD=PE,
∵P是OC上一点,PD⊥OA,PE⊥OB,
∴OC是∠AOB的平分线;
(2)∵PF∥OB,∠AOB=30°,
∴∠PFD=∠AOB=30°,
在Rt△PDF中,PD=![]() PF=2,
PF=2,
∴PE=PD=2.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目