题目内容
【题目】(教材回顾)课本88页,有这样一段文字:人们通过长期观察发现如果早晨天空中棉絮的高积云,那么午后常有雷雨降临,于是有了“朝有破絮云,午后雷雨临”的谚语.在数学的学习过程中,我们经常用这样的方法探究规律.
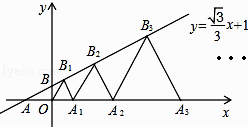
(数学问题)三角形有3个顶点,如果在它的内部再画n个点,并以这(n+3)个点为顶点画三角形,那么最多可以剪得多少个这样的三角形?
(问题探究)为了解决这个问题,我们可以从n=1,n=2,n=3等具体的、简单的情形入手,探索最多可以剪得的三角形个数的变化规律.
三角形内点的个数 | 图形 | 最多剪出的小三角形个数 |
1 |
| 3 |
2 |
| 5 |
3 |
| 7 |
… | … | … |
(问题解决)
(1) 当三角形内有4个点时,最多剪得的三角形个数为______________;
(2) 你发现的变化规律是:三角形内的点每增加1个,最多剪得的三角形增加______个;
(3) 猜想:当三角形内点的个数为n时,最多可以剪得_______________个三角形;
像这样通过对简单情形的观察、分析,从特殊到一般地探索这类现象的规律、提出猜想的思想方法称为归纳.
(问题拓展)
(4)请你尝试用归纳的方法探索1+3+5+7+…+(2n-1)+(2n+1)的和是多少?
【答案】(1)9;(2)2;(3)2n+1;(4)n2+2n+1.
【解析】
(1)利用表格中数据得出三角形个数的变化可推出n=4时,最多剪得的三角形的个数;
(2)利用(1)中数据得出三角形个数的变化规律即可;
(3)利用(2)中变化规律即可得出当三角形内点的个数为n时,最多可以剪得三角形的个数;
问题拓展:利用补项法求出答案.
(1)∵当三角形内点的个数为1时,最多可以剪得3个三角形;
当三角形内点的个数为2时,最多可以剪得5个三角形;
当三角形内点的个数为3时,最多可以剪得7个三角形;
∴当三角形内点的个数为4时,最多可以剪得9个三角形;
故答案为:9;
(2)由(1)的结果可得出:三角形内的点每增加1个,最多剪得的三角形增加2个;
故答案为:2;
(3)∵1×2+1=3,2×2+1=5,3×2+1=7,
∴当三角形内点的个数为n时,最多可以剪得(2n+1)个三角形;
故答案为:2n+1;
【问题拓展】
1+3+5+7+…+(2n-1)+(2n+1)
=![]() [1+3+5+7+…+(2n-1)+(2n+1)][(2n+1)+(2n-1)+…+7+5+3+1]
[1+3+5+7+…+(2n-1)+(2n+1)][(2n+1)+(2n-1)+…+7+5+3+1]
=![]() (n+1)(1+2n+1)
(n+1)(1+2n+1)
=(n+1)2
=n2+2n+1.

【题目】小文同学每天乘从BRT(城市快速公交)上学,为了方便乘坐BRT,他用自己勤工俭学的钱买了80元的公交卡.如果他乘坐的次数用n表示,则记录他每次乘坐BRT后公交卡的余额(单位:元)如下表:
次数n | 余额(元) |
1 | 80-0.9 |
2 | 80-1.8 |
3 | 80-2.7 |
4 | 80-3.6 |
… | … |
(1)写出用乘坐BRT的次数n表示余额的式子为____________________;
(2)利用(1)中的式子,帮助小文同学算一算,他一个月乘坐BRT有84次,这80元的公交卡够不够用,若够用,能剩多少元?
(3)小文同学用80元的公交卡最多能乘坐BRT__________________次.
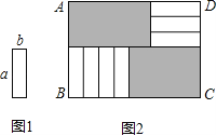
【题目】从边长为a的大正方形纸板中挖去一个边长为b的小正方形后,将其裁成四个相同的等腰梯形(如图1),然后拼成一个平行四边形(如图2)。那么通过计算两个图形的阴影部分的面积,可以验证成立的公式是( )
A.a2-b2=(a-b)2 | B.(a+b)2="a+2ab+b" |
C.(a-b)2=a2-2ab+b2 | D.a2-b2=(a-b)(a+b) |