题目内容
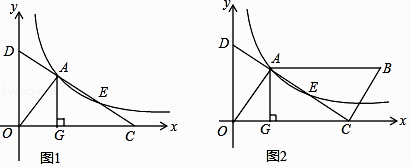
【题目】如图,图①中△ABC是等边三角形,其边长是3,图②中△DEF是等腰直角三角形,∠F=90°,DF=EF=3.
(1)若S1为△ABC的面积,S2为△DEF的面积,S3=![]() AB·BC·sinB,S4=
AB·BC·sinB,S4=![]() DE·DF·sinD,请通过计算说明S1与S3,S2与S4之间有着怎样的关系;
DE·DF·sinD,请通过计算说明S1与S3,S2与S4之间有着怎样的关系;
![]()
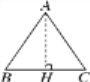
(2)在图③中,∠P=α(α为锐角),OP=m,PQ=n,△OPQ的面积为S,请你根据第(1)小题的解答,直接写出S与m,n以及α之间的关系式,并给出证明.
【答案】(1) S1=S3,S2=S4 (2) S=![]() mnsinα.
mnsinα.
【解析】(1)图①,过点A作AH⊥BC于点H,由已知先求出AH的长,再利用三角形面积公式进行计算可得S1;图②直接利用三角形面积公式进行求解可得S2;
根据已知数据可计算得出S3,计算S4时,先利用勾股定理求出DE的长,再代入式子进行计算即可,根据以上数据进行比较即可得;
(2)根据(1)中的发现直接写出然后进行证明即可得.证明思路:过点O作OM⊥PQ,垂足为点M,在Rt△OPM中,先求出OM长,再利用三角形面积公式进行计算即可得证.
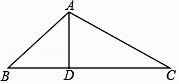
(1)如图,过点A作AH⊥BC于点H,
∵△ABC是等边三角形,AH⊥BC,∴AH=AB·sinB=3sin60°=3×![]() =
=![]() ,
,
∴S1=![]() ×3×
×3×![]() =
=![]() ,
,
∵△DEF是等腰直角三角形,∠F=90°,DF=EF=3,
∴∠D=45°,S2=![]() =
=![]() ,
,
S3=![]() AB·BC·sinB=
AB·BC·sinB=![]() ×3×3×sin60°=
×3×3×sin60°=![]() ,
,
在Rt△DEF中,由勾股定理得DE=![]() =3
=3![]() ,
,
∴S4=![]() DE·DF·sinD=
DE·DF·sinD=![]() ×3
×3![]() ×3×
×3×![]() =
=![]() ,
,
∴S1=S3,S2=S4;
(2)S=![]() mnsinα,证明如下:
mnsinα,证明如下:
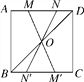
如图,过点O作OM⊥PQ,垂足为点M,
在Rt△OPM中,∠OMP=90°,∴OM=OP·sinP,
∵∠P=α,OP=m,∴OM=msinα,
∴S=![]() PQ·OM=
PQ·OM=![]() mnsinα.
mnsinα.

 名校课堂系列答案
名校课堂系列答案【题目】(教材回顾)课本88页,有这样一段文字:人们通过长期观察发现如果早晨天空中棉絮的高积云,那么午后常有雷雨降临,于是有了“朝有破絮云,午后雷雨临”的谚语.在数学的学习过程中,我们经常用这样的方法探究规律.
(数学问题)三角形有3个顶点,如果在它的内部再画n个点,并以这(n+3)个点为顶点画三角形,那么最多可以剪得多少个这样的三角形?
(问题探究)为了解决这个问题,我们可以从n=1,n=2,n=3等具体的、简单的情形入手,探索最多可以剪得的三角形个数的变化规律.
三角形内点的个数 | 图形 | 最多剪出的小三角形个数 |
1 |
| 3 |
2 |
| 5 |
3 |
| 7 |
… | … | … |
(问题解决)
(1) 当三角形内有4个点时,最多剪得的三角形个数为______________;
(2) 你发现的变化规律是:三角形内的点每增加1个,最多剪得的三角形增加______个;
(3) 猜想:当三角形内点的个数为n时,最多可以剪得_______________个三角形;
像这样通过对简单情形的观察、分析,从特殊到一般地探索这类现象的规律、提出猜想的思想方法称为归纳.
(问题拓展)
(4)请你尝试用归纳的方法探索1+3+5+7+…+(2n-1)+(2n+1)的和是多少?