题目内容
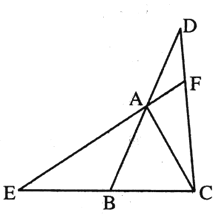
【题目】如图,在△ABC中,∠ABC=60°,AC=2AB,AD平分∠BAC交BC于点D,延长DB至点F,使BF=BD连接AF.
(1)求证:AF=CD.
(2)若CE平分∠ACB交AB于点E,试猜想AC,AF,AE三条线段之间的数量关系,并证明你的猜想.

【答案】(1)证明见解析;(2) AC=AF+AE,证明见解析
【解析】
(1)取AC的中点E,连接DE,根据题目已知条件可以证得△ABD≌△AED,再利用全等三角形的性质,可以证得△AFB≌△CDE,即可得出结论;
(2) 在AC上取一点M,使得AM=AE,根据AD是∠BAC的角平分线,CE是∠ACB的角平分线,可以得出∠AOE=60°,根据条件可以证得△AEO≌△AMO,利用全等三角形的性质可以证得△COD≌△COM,故可以得出结果.
(1)证明:如图所示,取AC的中点E,连接DE,
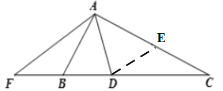
∵AC=2AB,
∴AB=AE=EC,
∵AD是∠BAC的角平分线,
∴∠BAD=∠DAC,
在△ABD和△AED中
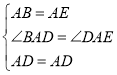
∴△ABD≌△AED,
∴∠ABD=∠AED,DB=DE,
∴∠ABF=∠DEC,
∵FB=BD,
∴FB=DE,
在△AFB和△CDE中
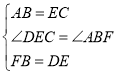
△AFB≌△CDE,
∴AF=DC.
(2)猜想:AC=AF+AE,
证明:如图所示,在AC上取一点M,使得AM=AE
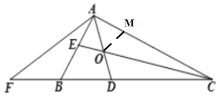
∵AD是∠BAC的角平分线,CE是∠ACB的角平分线,
∴∠BAD=∠DAC,∠ACE=∠ECB,
∵∠ABC=60°,
∴∠BAC+∠ACB=120°,
∴∠ACE+∠OAC=60°,
∴∠AOC=120°,
∴∠AOE=60°,
在△AEO和△AMO中
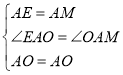
∴△AEO≌△AMO,
∴∠AOE=∠AOM=60°,
∴∠MOC=60°,
∵∠AOE=∠DOC,
∴∠DOC=60°,
在△COD和△COM中
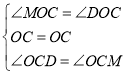
∴△COD≌△COM,
∴CM=CD,
由题(1)知CD=AF,
∴AF=CM,
∴AC=AM+MC=AE+AF.