题目内容
【题目】如图, ![]() 是等边三角形,延长
是等边三角形,延长![]() 到点
到点![]() ,延长
,延长![]() 到点
到点![]() ,使
,使![]() ,连接
,连接![]() ,延长
,延长![]() 交
交![]() 于
于![]() .
.
(1)求证: ![]() ;
;
(2)求![]() 的度数.
的度数.
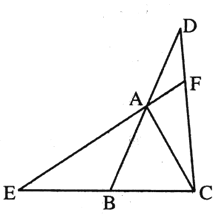
【答案】(1)证明见解析;(2)60°
【解析】
(1)根据等边三角形的性质得到AB=AC,∠DAC=∠ABE=120°,结合![]() 可证明△ABE≌△ACD,可得∠BAE=∠ACD,AE=CD,故可得∠EAC=∠DCB,,进一步可证明
可证明△ABE≌△ACD,可得∠BAE=∠ACD,AE=CD,故可得∠EAC=∠DCB,,进一步可证明![]() ;
;
(2)根据全等三角形的性质得到∠E=∠D,∠ EAB=∠DAF,根据三角形的外角的性质得到结论.
(1)证明:∵△ABC是等边三角形,
∴AB=AC,∠CAB=∠ABC=60°,
∴∠DAC=∠ABE=120°,
在△ABE和△ACD中,
 ,
,
∴△ABE≌△ACD,
∴AE=CD,∠BAE=∠ACD,
∴∠CAE=∠BCD,
在△ACE和△CBD中
 ,
,
∴![]() ;
;
(2)∵△ABE≌△ACD,
∴∠E=∠D,
∴∠CFE=∠D+∠DAF
=∠E+∠EAB,
=∠ABC,
=60°.

练习册系列答案
相关题目